المرجع الألكتروني للمعلوماتية
القرآن الكريم وعلومه
العقائد الإسلامية
الفقه وأصوله 
الرجال والحديث 
سيرة الرسول وآله 
علوم اللغة العربية 
الأدب العربي 
الأسرة والمجتمع 
الأخلاق والأدعية 
التاريخ 
الادارة والاقتصاد 
علم الفيزياء 
علم الكيمياء 
علم الأحياء 
الرياضيات 
الهندسة المدنية 
الزراعة 
الجغرافية 
القانون 
اللغة الأنكليزية 
الأخبار 
الإعلام 
مكتبة الصور 
أقلام بمختلف الألوان 
إضاءات
مفتاح
أجوبة الإستفتاءات الشرعية
وثائقيات
تاريخ الرياضيات
الرياضيات في الحضارات المختلفة
الرياضيات المتقطعة
الجبر
الهندسة
المعادلات التفاضلية و التكاملية
التحليل
علماء الرياضيات | q-Beta Function |
 1491
 07:04 مساءً
date: 26-8-2019 |
Author : Andrews, G. E. 
Book or Source : q-Series: Their Development and Application in Analysis, Number Theory, Combinatorics, Physics, and Computer Algebra. Providence, RI: Amer. Math.... 
Page and Part : ...|
Read More
Date: 26-8-2019
1492
Date: 22-4-2019
1865
Date: 24-9-2019
1491
|
A q-analog of the beta function
 |
 |
 |
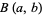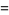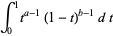(1) |
 |
 |
 |
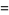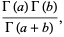(2) |
where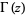 
is a gamma function, is given by
 |
 |
 |
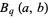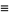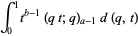(3) |
 |
 |
 |
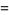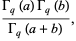(4) |
where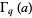 
is a q-gamma function, 
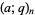is a q-Pochhammer symbol coefficient, and
 |
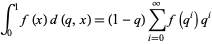(5) |
is a q-integral (Andrews 1986, pp. 11-12).
REFERENCES:
Andrews, G. E. q-Series: Their Development and Application in Analysis, Number Theory, Combinatorics, Physics, and Computer Algebra. Providence, RI: Amer. Math. Soc., 1986.
|
|
|
|
دراسة يابانية لتقليل مخاطر أمراض المواليد منخفضي الوزن
|
|
|
|
|
|
|
اكتشاف أكبر مرجان في العالم قبالة سواحل جزر سليمان
|
|
|
|
|
|
|
اتحاد كليات الطب الملكية البريطانية يشيد بالمستوى العلمي لطلبة جامعة العميد وبيئتها التعليمية
|
|
|
