المرجع الألكتروني للمعلوماتية
القرآن الكريم وعلومه
العقائد الإسلامية
الفقه وأصوله 
الرجال والحديث 
سيرة الرسول وآله 
علوم اللغة العربية 
الأدب العربي 
الأسرة والمجتمع 
الأخلاق والأدعية 
التاريخ 
الادارة والاقتصاد 
علم الفيزياء 
علم الكيمياء 
علم الأحياء 
الرياضيات 
الهندسة المدنية 
الزراعة 
الجغرافية 
القانون 
اللغة الأنكليزية 
الأخبار 
الإعلام 
مكتبة الصور 
أقلام بمختلف الألوان 
إضاءات
مفتاح
أجوبة الإستفتاءات الشرعية
وثائقيات
تاريخ الرياضيات
الرياضيات في الحضارات المختلفة
الرياضيات المتقطعة
الجبر
الهندسة
المعادلات التفاضلية و التكاملية
التحليل
علماء الرياضيات | Trilogarithm |
 1500
 04:19 مساءً
date: 13-8-2019 |
Author : Bailey, D. H.; Borwein, P. B.; and Plouffe, S 
Book or Source : "On the Rapid Computation of Various Polylogarithmic Constants." Math. Comput. 66 
Page and Part : ...|
Read More
Date: 25-8-2018
2591
Date: 21-8-2018
1154
Date: 22-5-2019
3781
|
 |
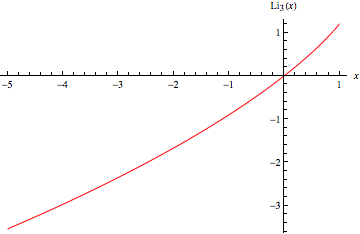The trilogarithm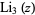 
, sometimes also denoted 
, is special case of the polylogarithm 
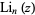for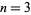 
. Note that the notation 
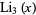for the trilogarithm is unfortunately similar to that for the logarithmic integral 
.
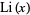The trilogarithm is implemented in the Wolfram Language as PolyLog[3, z].
 |
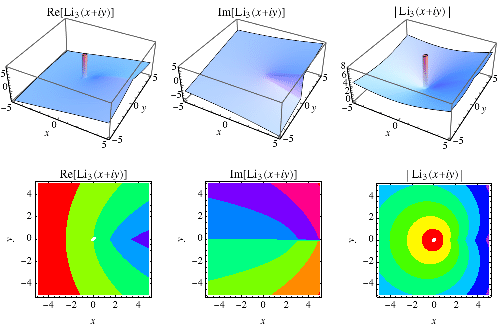Plots of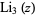 
in the complex plane are illustrated above.
Functional equations for the trilogarithm include
 |
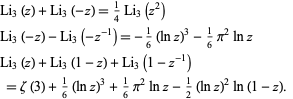(1) |
Analytic values for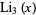 
include
![Li_3(-1)=-3/4zeta(3)
Li_3(0)=0
Li_3(1/2)=1/(24)[-2pi^2ln2+4(ln2)^3+21zeta(3)]
Li_3(1)=zeta(3)
Li_3(phi^(-2))=4/5zeta(3)+2/3(lnphi)^3-2/(15)pi^2lnphi](http://mathworld.wolfram.com/images/equations/Trilogarithm/NumberedEquation2.gif) |
(2) |
where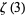 
is Apéry's constant and 
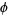is the golden ratio.
Bailey et al. showed that
 |
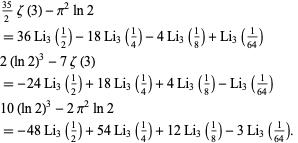(3) |
REFERENCES:
Bailey, D. H.; Borwein, P. B.; and Plouffe, S. "On the Rapid Computation of Various Polylogarithmic Constants." Math. Comput. 66, 903-913, 1997.
Lewin, L. Polylogarithms and Associated Functions. New York: North-Holland, pp. 154-156, 1981.
|
|
|
|
"عادة ليلية" قد تكون المفتاح للوقاية من الخرف
|
|
|
|
|
|
|
ممتص الصدمات: طريقة عمله وأهميته وأبرز علامات تلفه
|
|
|
|
|
|
|
المجمع العلمي للقرآن الكريم يقيم جلسة حوارية لطلبة جامعة الكوفة
|
|
|
