


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 9-9-2019
Date: 22-9-2019
Date: 18-8-2018
|
A function that arises in performance analysis of partially coherent, differentially coherent, and noncoherent communications. The generalized Marcum 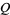 -function is defined by
-function is defined by
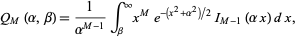 |
(1) |
where 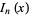 is a modified Bessel function of the first kind. It also has the series form
is a modified Bessel function of the first kind. It also has the series form
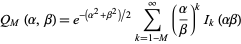 |
(2) |
(Helstrom 1960, Proakis 1983).
The Marcum 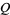 -function is implemented in the Wolfram Language as MarcumQ[M, a, b].
-function is implemented in the Wolfram Language as MarcumQ[M, a, b].
A special case is given by
![Q_1(alpha,alpha)=1/2[1+e^(-alpha^2)I_0(alpha^2)]](http://mathworld.wolfram.com/images/equations/MarcumQ-Function/NumberedEquation3.gif) |
(3) |
(Schwarz et al. 1966, eqn. A-3-2).
The Marcum 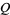 -function satisfies the identity
-function satisfies the identity
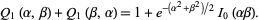 |
(4) |
The derivative of 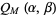 with respect to
with respect to 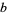 is given by
is given by
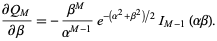 |
(5) |
REFERENCES:
Cantrell, P. E. and Ojha, A. K. "Comparison of Generalized 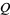 -Function Algorithms." IEEE Trans. Info. Th. 33, 591-596, Jul. 1987.
-Function Algorithms." IEEE Trans. Info. Th. 33, 591-596, Jul. 1987.
Helstrom, C. W. Statistical Theory of Signal Detection. New York: Pergamon, 1960.
Marcum, J. I. Table of Q Functions. U.S. Air Force RAND Research Memorandum M-339. Santa Monica, CA: Rand Corporation, Jan. 1, 1950.
Parl, S. "A New Method of Calculating the Generalized 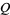 Function." IEEE Trans. Info. Th. 26, 121-124, Jan. 1980.
Function." IEEE Trans. Info. Th. 26, 121-124, Jan. 1980.
Peterson, R. L.; Ziemer, R. E.; and Borth, D. E. "Numerical Approximations for the Chi-Squared Probability Distribution and Marcum's 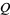 -Function." Appendix F in Introduction to Spread-Spectrum Communications. Englewood Cliffs, NJ: Prentice-Hall, pp. 672-681, 1995.
-Function." Appendix F in Introduction to Spread-Spectrum Communications. Englewood Cliffs, NJ: Prentice-Hall, pp. 672-681, 1995.
Proakis, J. Digital Communications. New York: McGraw-Hill, 1983.
Schwartz, M.; Bennett, W. R.; and Stein, S. Communication Systems and Techniques. New York: McGraw-Hill, 1966.
Shnidman, D. A. "The Calculation of the Probability of Detection and the Generalized Marcum 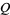 -Function." IEEE Trans. Info. Th. 35, 389-400, Mar. 1989.
-Function." IEEE Trans. Info. Th. 35, 389-400, Mar. 1989.
Simon, M. K. "A New Twist on the Marcum 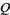 -Function and Its Application." IEEE Commun. Lett. 2, 39-41, Feb. 1998.
-Function and Its Application." IEEE Commun. Lett. 2, 39-41, Feb. 1998.
Simon, M. K. "The Nuttall 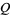 -Function: Its Relation to the Marcum
-Function: Its Relation to the Marcum 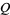 -Function and Its Application in Digital Communication Performance Evaluation." IEEE Trans. Commun. 50, 1712-1715, 2002.
-Function and Its Application in Digital Communication Performance Evaluation." IEEE Trans. Commun. 50, 1712-1715, 2002.
Simon, M. K. and Alouini, M.-S. "Exponential-Type Bounds on the Generalized Marcum 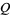 -function with Application to Error Probability Analysis over Fading Channels." IEEE Trans. Commun. 48, 359-366, Mar. 2000.
-function with Application to Error Probability Analysis over Fading Channels." IEEE Trans. Commun. 48, 359-366, Mar. 2000.
Simon, M. K. and Alouini, M.-S. Digital Communication over Fading Channels: A Unified Approach to Performance Analysis. New York: Wiley, 2000.
Simon, M. K.; Hinedi, S. M.; and Lindsey, W. C. Digital Communication Techniques: Signal Design and Detection. Englewood Cliffs, NJ: Prentice-Hall, 1965.
Stein, S. "Unified Analysis of Certain Coherent and Noncoherent Binary Communication Systems." IEEE Trans. Information Th. 10, 43-51, Jan. 1964.
Van Trees, H. L. Detection, Estimation, and Modulation Theory, Part I. New York: Wiley, pp. 394-395 and 411, 1968.



|
|
|
|
"عادة ليلية" قد تكون المفتاح للوقاية من الخرف
|
|
|
|
|
|
|
ممتص الصدمات: طريقة عمله وأهميته وأبرز علامات تلفه
|
|
|
|
|
|
|
المجمع العلمي للقرآن الكريم يقيم جلسة حوارية لطلبة جامعة الكوفة
|
|
|