المرجع الألكتروني للمعلوماتية
القرآن الكريم وعلومه
العقائد الإسلامية
الفقه وأصوله 
الرجال والحديث 
سيرة الرسول وآله 
علوم اللغة العربية 
الأدب العربي 
الأسرة والمجتمع 
الأخلاق والأدعية 
التاريخ 
الادارة والاقتصاد 
علم الفيزياء 
علم الكيمياء 
علم الأحياء 
الرياضيات 
الهندسة المدنية 
الزراعة 
الجغرافية 
القانون 
اللغة الأنكليزية 
الأخبار 
الإعلام 
مكتبة الصور 
أقلام بمختلف الألوان 
إضاءات
مفتاح
أجوبة الإستفتاءات الشرعية
وثائقيات
تاريخ الرياضيات
الرياضيات في الحضارات المختلفة
الرياضيات المتقطعة
الجبر
الهندسة
المعادلات التفاضلية و التكاملية
التحليل
علماء الرياضيات | MacRobert,s E-Function |
 2531
 03:54 مساءً
date: 17-6-2019 |
Author : Erdélyi, A.; Magnus, W.; Oberhettinger, F.; and Tricomi, F. G. 
Book or Source : "Definition of the E-Function." §5.2 in Higher Transcendental Functions, Vol. 1. New York: Krieger 
Page and Part : ...|
Read More
Date: 27-4-2018
1871
Date: 10-10-2019
1676
Date: 24-9-2018
1377
|
![E(p;alpha_r:rho_s:x)=(Gamma(alpha_(q+1)))/(Gamma(rho_1-alpha_1)Gamma(rho_2-alpha_2)...Gamma(rho_q-alpha_q))product_(mu=1)^qint_0^inftylambda_mu^(rho_mu-alpha_mu-1)(1+lambda_mu)^(-rho_mu)dlambda_muproduct_(nu=2)^(p-q-1)int_0^inftye^(-lambda_(q+nu))lambda_(q+nu)^(alpha_(q+nu)-1)dlambda_(q+nu)int_0^inftye^(-lambda_p)lambda_p^(alpha_p-1)[1+(lambda_(q+2)lambda_(q+3)...lambda_p)/((1+lambda_1)...(1+lambda_q)x)]^(-alpha_q+1)dlambda_p,](http://mathworld.wolfram.com/images/equations/MacRobertsE-Function/NumberedEquation1.gif) |
where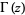 
is the gamma function and other details are discussed by Gradshteyn and Ryzhik (2000).
REFERENCES:
Erdélyi, A.; Magnus, W.; Oberhettinger, F.; and Tricomi, F. G. "Definition of the E-Function." §5.2 in Higher Transcendental Functions, Vol. 1. New York: Krieger, pp. 203-206, 1981.
Gradshteyn, I. S. and Ryzhik, I. M. Tables of Integrals, Series, and Products, 6th ed. San Diego, CA: Academic Press, pp. 896-903 and 1071-1072, 2000.
MacRobert, T. M. "Induction Proofs of the Relations between Certain Asymptotic Expansions and Corresponding Generalised Hypergeometric Series." Proc. Roy. Soc. Edinburgh 58, 1-13, 1937-38.
MacRobert, T. M. "Some Formulæ for the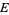 
-Function." Philos. Mag. 31, 254-260, 1941.
|
|
|
|
علامات بسيطة في جسدك قد تنذر بمرض "قاتل"
|
|
|
|
|
|
|
أول صور ثلاثية الأبعاد للغدة الزعترية البشرية
|
|
|
|
|
|
|
بمشاركة 800 طالبة.. معهد القرآن الكريم النسوي يختتم برامجه للمتخرجات في الدورات القرآنية الصيفية
|
|
|
