المرجع الألكتروني للمعلوماتية
القرآن الكريم وعلومه
العقائد الإسلامية
الفقه وأصوله 
الرجال والحديث 
سيرة الرسول وآله 
علوم اللغة العربية 
الأدب العربي 
الأسرة والمجتمع 
الأخلاق والأدعية 
التاريخ 
الادارة والاقتصاد 
علم الفيزياء 
علم الكيمياء 
علم الأحياء 
الرياضيات 
الهندسة المدنية 
الزراعة 
الجغرافية 
القانون 
اللغة الأنكليزية 
الأخبار 
الإعلام 
مكتبة الصور 
أقلام بمختلف الألوان 
إضاءات
مفتاح
أجوبة الإستفتاءات الشرعية
وثائقيات
تاريخ الرياضيات
الرياضيات في الحضارات المختلفة
الرياضيات المتقطعة
الجبر
الهندسة
المعادلات التفاضلية و التكاملية
التحليل
علماء الرياضيات | Tetrachoric Function |
 1248
 02:13 صباحاً
date: 28-4-2019 |
Author : Kenney, J. F. and Keeping, E. S. 
Book or Source : "Tetrachoric Correlation." §8.5 in Mathematics of Statistics, Pt. 2, 2nd ed. Princeton, NJ: Van Nostrand 
Page and Part : pp. 205-207|
Read More
Date: 29-9-2018
1369
Date: 24-9-2019
991
Date: 14-10-2019
2733
|
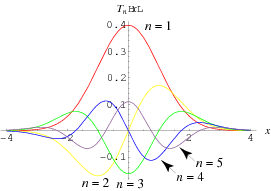
The function defined by
 |
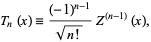where
 |
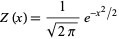and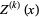 
is the 
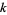th derivative of 
.
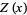REFERENCES:
Kenney, J. F. and Keeping, E. S. "Tetrachoric Correlation." §8.5 in Mathematics of Statistics, Pt. 2, 2nd ed. Princeton, NJ: Van Nostrand, pp. 205-207, 1951.
|
|
|
|
مخاطر عدم علاج ارتفاع ضغط الدم
|
|
|
|
|
|
|
اختراق جديد في علاج سرطان البروستات العدواني
|
|
|
|
|
|
|
نشر مظاهر الفرح في مرقد أبي الفضل العباس بذكرى ولادة السيدة زينب (عليهما السلام)
|
|
|
