Elliptic Invariants

The invariants of a Weierstrass elliptic function 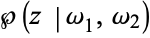 are defined by the Eisenstein series

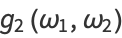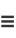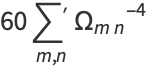			(1)
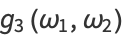			(2)

Here,

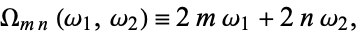(3)

where 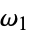 and 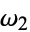 are the half-periods of the elliptic function. The Wolfram Language command WeierstrassInvariants[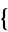omega1, omega2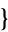] gives the invariants  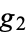and 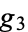 corresponding to the half-periods 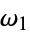and .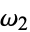

Writing ,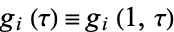

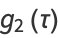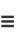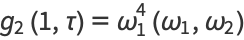			(4)
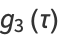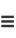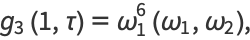			(5)

and the invariants have the Fourier series

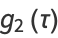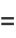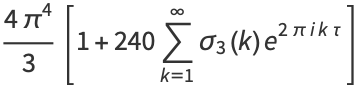			(6)
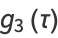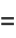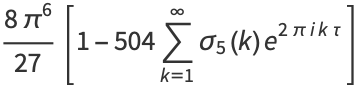			(7)

where 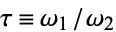 is the half-period ratio and  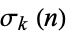is the divisor function (Apostol 1997).

REFERENCES:

Apostol, T. M. "The Fourier Expansions of 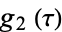 and 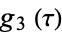." §1.9 in Modular Functions and Dirichlet Series in Number Theory, 2nd ed. New York: Springer-Verlag, pp. 12-13, 1997.

Brezhnev, Y. V. "Uniformisation: On the Burnside Curve 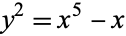." 9 Dec 2001. http://arxiv.org/abs/math.CA/0111150.