Rayleigh Function

The Rayleigh functions 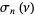 for 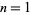, 2, ..., are defined as

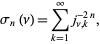where 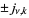 are the zeros of the Bessel function of the first kind  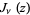(Watson 1966, p. 502; Gupta and Muldoon 1999). They were used by Euler, Rayleigh, and others to evaluate zeros of Bessel functions.

There is a convolution formula connecting Rayleigh functions of different orders,

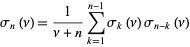(Kishore 1963, Gupta and Muldoon 1999).

REFERENCES:

Gupta, D. P. and Muldoon, M. E. "Riccati Equations and Convolution Formulas for Functions of Rayleigh Type." 24 Oct 1999. http://arxiv.org/abs/math.CA/9910128.

Ismail, M. E. H. and Muldoon, M. E. "Bounds for the Small Real and Purely Imaginary Zeros of Bessel and Related Functions." Meth. Appl. Anal. 2, 1-21, 1995.

Kishore, N. "The Rayleigh Function." Proc. Amer. Math. Soc. 14, 527-533, 1963.

Obi, E. C. "The Complete Monotonicity of the Rayleigh Function." J. Math. Anal. Appl. 77, 465-468, 1980.

Watson, G. N. A Treatise on the Theory of Bessel Functions, 2nd ed. Cambridge, England: Cambridge University Press, 1966.