المرجع الألكتروني للمعلوماتية
القرآن الكريم وعلومه
العقائد الإسلامية
الفقه وأصوله 
الرجال والحديث 
سيرة الرسول وآله 
علوم اللغة العربية 
الأدب العربي 
الأسرة والمجتمع 
الأخلاق والأدعية 
التاريخ 
الادارة والاقتصاد 
علم الفيزياء 
علم الكيمياء 
علم الأحياء 
الرياضيات 
الهندسة المدنية 
الزراعة 
الجغرافية 
القانون 
اللغة الأنكليزية 
الأخبار 
الإعلام 
مكتبة الصور 
أقلام بمختلف الألوان 
إضاءات
مفتاح
أجوبة الإستفتاءات الشرعية
وثائقيات
تاريخ الرياضيات
الرياضيات في الحضارات المختلفة
الرياضيات المتقطعة
الجبر
الهندسة
المعادلات التفاضلية و التكاملية
التحليل
علماء الرياضيات | Wilson Polynomial |
 1108
 04:16 مساءً
date: 23-9-2019 |
Author : oekoek, R. and Swarttouw, R. F. 
Book or Source : Wilson." §1.1 in The Askey-Scheme of Hypergeometric Orthogonal Polynomials and its q-Analogue. Delft, Netherlands: Technische Universiteit Delft,... 
Page and Part : ...|
Read More
Date: 16-4-2019
3066
Date: 24-9-2018
2083
Date: 18-8-2018
2873
|
The orthogonal polynomials defined variously by
 |
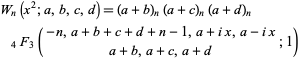(1) |
(Koekoek and Swarttouw 1998, p. 24) or
 |
 |
 |
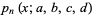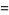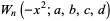(2) |
 |
 |
 |
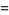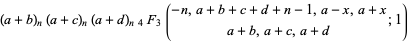(3) |
(Koepf, p. 116, 1998).
The first few are
 |
 |
 |
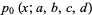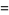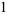(4) |
 |
 |
 |
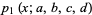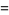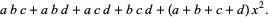(5) |
The Wilson polynomials obey the identity
 |
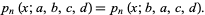(6) |
REFERENCES:
Koekoek, R. and Swarttouw, R. F. "Wilson." §1.1 in The Askey-Scheme of Hypergeometric Orthogonal Polynomials and its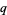 
-Analogue. Delft, Netherlands: Technische Universiteit Delft, Faculty of Technical Mathematics and Informatics Report 98-17, pp. 24-26, 1998.
Koepf, W. Hypergeometric Summation: An Algorithmic Approach to Summation and Special Function Identities. Braunschweig, Germany: Vieweg, p. 116, 1998.
Wilson, J. A. "Some Hypergeometric Orthogonal Polynomials." SIAM J. Math. Anal. 11, 690-701, 1980.
|
|
|
|
أكبر مسؤول طبي بريطاني: لهذا السبب يعيش الأطفال حياة أقصر
|
|
|
|
|
|
|
طريقة مبتكرة لمكافحة الفيروسات المهددة للبشرية
|
|
|
|
|
|
|
أكاديميون: نظام مسار بولونيا يسهم في تحسين جودة التعليم بالجامعات العراقية
|
|
|
