


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 2-10-2019
Date: 29-9-2019
Date: 30-3-2019
|
Given a set  of
of  equations in
equations in  variables
variables  , ...,
, ...,  , written explicitly as
, written explicitly as
![y=[f_1(x); f_2(x); |; f_n(x)],](http://mathworld.wolfram.com/images/equations/Jacobian/NumberedEquation1.gif) |
(1) |
or more explicitly as
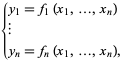 |
(2) |
the Jacobian matrix, sometimes simply called "the Jacobian" (Simon and Blume 1994) is defined by
![J(x_1,...,x_n)=[(partialy_1)/(partialx_1) ... (partialy_1)/(partialx_n); | ... |; (partialy_n)/(partialx_1) ... (partialy_n)/(partialx_n)].](http://mathworld.wolfram.com/images/equations/Jacobian/NumberedEquation3.gif) |
(3) |
The determinant of  is the Jacobian determinant (confusingly, often called "the Jacobian" as well) and is denoted
is the Jacobian determinant (confusingly, often called "the Jacobian" as well) and is denoted
 |
(4) |
The Jacobian matrix and determinant can be computed in the Wolfram Language using
JacobianMatrix[f_List?VectorQ, x_List] :=
Outer[D, f, x] /; Equal @@ (Dimensions /@ {f, x})
JacobianDeterminant[f_List?VectorQ, x_List] :=
Det[JacobianMatrix[f, x]] /;
Equal @@ (Dimensions /@ {f, x})
Taking the differential
 |
(5) |
shows that  is the determinant of the matrix
is the determinant of the matrix  , and therefore gives the ratios of
, and therefore gives the ratios of  -dimensional volumes (contents) in
-dimensional volumes (contents) in  and
and  ,
,
 |
(6) |
It therefore appears, for example, in the change of variables theorem.
The concept of the Jacobian can also be applied to  functions in more than
functions in more than  variables. For example, considering
variables. For example, considering  and
and  , the Jacobians
, the Jacobians
 |
 |
 |
(7) |
 |
 |
 |
(8) |
can be defined (Kaplan 1984, p. 99).
For the case of  variables, the Jacobian takes the special form
variables, the Jacobian takes the special form
 |
(9) |
where  is the dot product and
is the dot product and  is the cross product, which can be expanded to give
is the cross product, which can be expanded to give
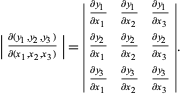 |
(10) |
REFERENCES:
Gradshteyn, I. S. and Ryzhik, I. M. "Jacobian Determinant." §14.313 in Tables of Integrals, Series, and Products, 6th ed. San Diego, CA: Academic Press, pp. 1068-1069, 2000.
Kaplan, W. Advanced Calculus, 3rd ed. Reading, MA: Addison-Wesley, pp. 98-99, 123, and 238-245, 1984.
Simon, C. P. and Blume, L. E. Mathematics for Economists. New York: W. W. Norton, 1994.



|
|
|
|
التوتر والسرطان.. علماء يحذرون من "صلة خطيرة"
|
|
|
|
|
|
|
مرآة السيارة: مدى دقة عكسها للصورة الصحيحة
|
|
|
|
|
|
|
اللجنة العلمية لمؤتمر ذاكرة الألم: اعتماد معايير رصينة لتقييم البحوث المشاركة
|
|
|