


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 8-3-2017
Date: 13-2-2019
Date: 23-1-2019
|
Let any finite or infinite set of points having no finite limit point be prescribed, and associate with each of its points a definite positive integer as its order. Then there exists an entire function which has zeros to the prescribed orders at precisely the prescribed points, and is otherwise different from zero. Moreover, this function can be represented as a product from which one can read off again the positions and orders of the zeros. Furthermore, if 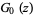 is one such function, then
is one such function, then
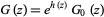 |
is the most general function satisfying the conditions of the problem, where 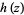 denotes an arbitrary entire function.
denotes an arbitrary entire function.
This theorem is also sometimes simply known as Weierstrass's theorem. A spectacular example is given by the Hadamard product.
REFERENCES:
Knopp, K. "Weierstrass's Factor-Theorem." §1 in Theory of Functions Parts I and II, Two Volumes Bound as One, Part II. New York: Dover, pp. 1-7, 1996.
Krantz, S. G. "The Weierstrass Factorization Theorem." §8.2 in Handbook of Complex Variables. Boston, MA: Birkhäuser, pp. 109-110, 1999.



|
|
|
|
دخلت غرفة فنسيت ماذا تريد من داخلها.. خبير يفسر الحالة
|
|
|
|
|
|
|
ثورة طبية.. ابتكار أصغر جهاز لتنظيم ضربات القلب في العالم
|
|
|
|
|
|
|
قسم شؤون المعارف ووفد من جامعة البصرة يبحثان سبل تعزيز التعاون المشترك
|
|
|