
آخر المواضيع المضافة


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 30-12-2018
Date: 23-12-2018
Date: 11-6-2018
|
The integral kernel in the Poisson integral, given by
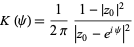 |
(1) |
for the open unit disk 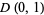 . Writing
. Writing 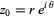 and taking
and taking 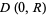 gives
gives
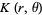 |
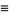 |
![1/(2pi)R[(R+re^(itheta))/(R-re^(itheta))]](http://mathworld.wolfram.com/images/equations/PoissonKernel/Inline6.gif) |
(2) |
 |
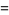 |
![1/(2pi)R[((R+re^(itheta))(R-re^(-itheta)))/((R-re^(itheta))(R-re^(-itheta)))]](http://mathworld.wolfram.com/images/equations/PoissonKernel/Inline9.gif) |
(3) |
 |
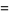 |
![1/(2pi)R[(R^2-rR(e^(itheta)-e^(-itheta))-r^2)/(R^2-rR(e^(itheta)+e^(-itheta))+r^2)]](http://mathworld.wolfram.com/images/equations/PoissonKernel/Inline12.gif) |
(4) |
 |
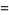 |
![1/(2pi)R[(R^2+2irRsintheta-r^2)/(R^2-2Rrcostheta+r^2)]](http://mathworld.wolfram.com/images/equations/PoissonKernel/Inline15.gif) |
(5) |
 |
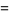 |
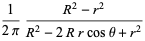 |
(6) |
(Krantz 1999, p. 93).
In three dimensions,
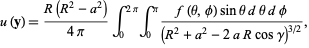 |
(7) |
where 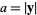 and
and
![cosgamma=y·[Rcosthetasinphi; Rsinthetasinphi; Rcosphi].](http://mathworld.wolfram.com/images/equations/PoissonKernel/NumberedEquation3.gif) |
(8) |
The Poisson kernel for the 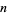 -ball is
-ball is
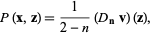 |
(9) |
where 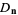 is the outward normal derivative at point
is the outward normal derivative at point 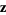 on a unit
on a unit 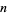 -sphere and
-sphere and
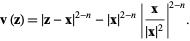 |
(10) |
Let 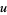 be harmonic on a neighborhood of the closed unit disk
be harmonic on a neighborhood of the closed unit disk 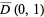 , then the reproducing property of the Poisson kernel states that for
, then the reproducing property of the Poisson kernel states that for 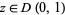 ,
,
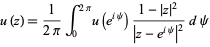 |
(11) |
(Krantz 1999, p. 94).
REFERENCES:
Gradshteyn, I. S. and Ryzhik, I. M. Tables of Integrals, Series, and Products, 6th ed. San Diego, CA: Academic Press, p. 1090, 2000.
Krantz, S. G. "The Poisson Kernel." §7.3.2 in Handbook of Complex Variables. Boston, MA: Birkhäuser, p. 93, 1999.



|
|
|
|
دراسة يابانية لتقليل مخاطر أمراض المواليد منخفضي الوزن
|
|
|
|
|
|
|
اكتشاف أكبر مرجان في العالم قبالة سواحل جزر سليمان
|
|
|
|
|
|
|
اتحاد كليات الطب الملكية البريطانية يشيد بالمستوى العلمي لطلبة جامعة العميد وبيئتها التعليمية
|
|
|