Abel-Plana Formula

The Abel-Plana formula gives an expression for the difference between a discrete sum and the corresponding integral. The formula can be derived from the argument principle

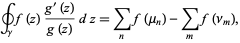(1)

where 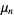 are the zeros of  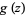and 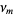 are the poles contained within the contour 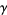. An appropriate choice of  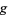and 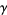then yields

(2)

or equivalently

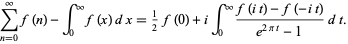(3)

The formula is particularly useful in Casimir effect calculations involving differences between quantized modes and free modes.

REFERENCES:

Mostepanenko, V. M. and Trunov, N. N. §2.2 in The Casimir Effect and Its Applications. Oxford, England: Clarendon Press, 1997.

Saharian, A. A. "The Generalized Abel-Plana Formula. Applications to Bessel Functions and Casimir Effect." http://www.ictp.trieste.it/~pub_off/preprints-sources/2000/IC2000014P.pdf.