


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 17-11-2018
Date: 18-12-2018
Date: 24-10-2018
|
 |
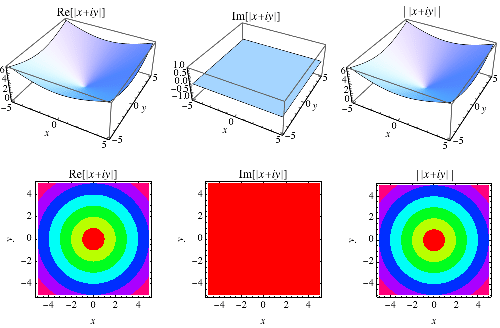 |
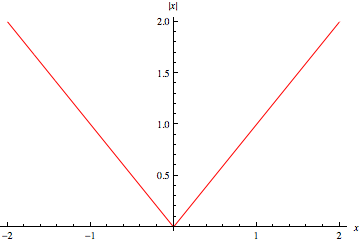
The modulus of a complex number 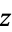 , also called the complex norm, is denoted
, also called the complex norm, is denoted 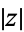 and defined by
and defined by
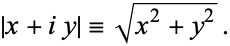 |
(1) |
If 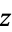 is expressed as a complex exponential (i.e., a phasor), then
is expressed as a complex exponential (i.e., a phasor), then
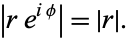 |
(2) |
The complex modulus is implemented in the Wolfram Language as Abs[z], or as Norm[z].
The square 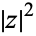 of
of 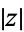 is sometimes called the absolute square.
is sometimes called the absolute square.
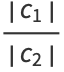
Let 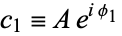 and
and 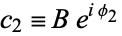 be two complex numbers. Then
be two complex numbers. Then
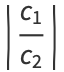 |
 |
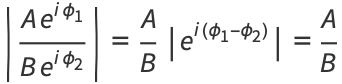 |
(3) |
 |
 |
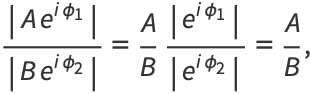 |
(4) |
so
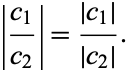 |
(5) |
Also,
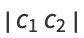 |
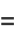 |
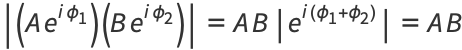 |
(6) |
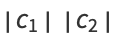 |
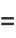 |
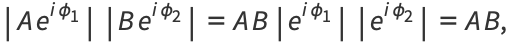 |
(7) |
so
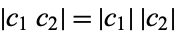 |
(8) |
and, by extension,
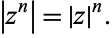 |
(9) |
The only functions satisfying identities of the form
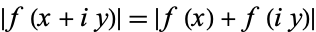 |
(10) |
are 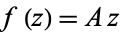 ,
, 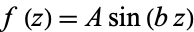 , and
, and 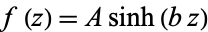 (Robinson 1957).
(Robinson 1957).
REFERENCES:
Abramowitz, M. and Stegun, I. A. (Eds.). Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, p. 16, 1972.
Krantz, S. G. "Modulus of a Complex Number." §1.1.4 n Handbook of Complex Variables. Boston, MA: Birkhäuser, pp. 2-3, 1999.
Robinson, R. M. "A Curious Mathematical Identity." Amer. Math. Monthly 64, 83-85, 1957.



|
|
|
|
التوتر والسرطان.. علماء يحذرون من "صلة خطيرة"
|
|
|
|
|
|
|
مرآة السيارة: مدى دقة عكسها للصورة الصحيحة
|
|
|
|
|
|
|
نحو شراكة وطنية متكاملة.. الأمين العام للعتبة الحسينية يبحث مع وكيل وزارة الخارجية آفاق التعاون المؤسسي
|
|
|