Complex Differentiable

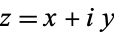Let  and 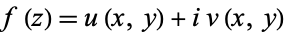 on some region  containing the point . If 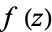 satisfies the Cauchy-Riemann equations and has continuous first partial derivatives in the neighborhood of 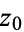, then  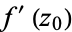exists and is given by

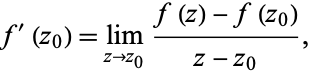and the function is said to be complex differentiable (or, equivalently, analytic or holomorphic).

A function 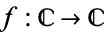 can be thought of as a map from the plane to the plane, 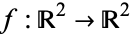. Then  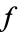is complex differentiable iff its Jacobian is of the form

at every point. That is, its derivative is given by the multiplication of a complex number 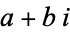. For instance, the function 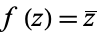, where  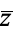is the complex conjugate, is not complex differentiable.

REFERENCES:

Shilov, G. E. Elementary Real and Complex Analysis. New York: Dover, p. 379, 1996.