


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 19-9-2018
Date: 13-8-2018
Date: 23-9-2019
|
Lagrange multipliers, also called Lagrangian multipliers (e.g., Arfken 1985, p. 945), can be used to find the extrema of a multivariate function 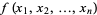 subject to the constraint
subject to the constraint 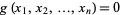 , where
, where 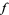 and
and 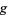 are functions with continuous first partial derivatives on the open set containing the curve
are functions with continuous first partial derivatives on the open set containing the curve 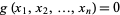 , and
, and 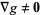 at any point on the curve (where
at any point on the curve (where 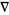 is the gradient).
is the gradient).
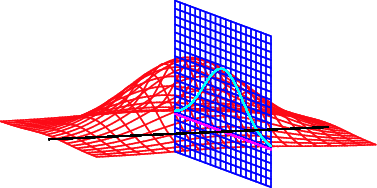
For an extremum of 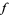 to exist on
to exist on 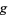 , the gradient of
, the gradient of 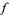 must line up with the gradient of
must line up with the gradient of 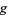 . In the illustration above,
. In the illustration above, 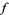 is shown in red,
is shown in red, 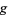 in blue, and the intersection of
in blue, and the intersection of 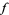 and
and 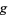 is indicated in light blue. The gradient is a horizontal vector (i.e., it has no
is indicated in light blue. The gradient is a horizontal vector (i.e., it has no 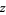 -component) that shows the direction that the function increases; for
-component) that shows the direction that the function increases; for 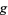 it is perpendicular to the curve, which is a straight line in this case. If the two gradients are in the same direction, then one is a multiple (
it is perpendicular to the curve, which is a straight line in this case. If the two gradients are in the same direction, then one is a multiple (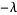 ) of the other, so
) of the other, so
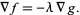 |
(1) |
The two vectors are equal, so all of their components are as well, giving
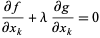 |
(2) |
for all 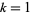 , ...,
, ..., 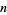 , where the constant
, where the constant 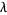 is called the Lagrange multiplier.
is called the Lagrange multiplier.
The extremum is then found by solving the 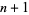 equations in
equations in 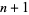 unknowns, which is done without inverting
unknowns, which is done without inverting 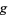 , which is why Lagrange multipliers can be so useful.
, which is why Lagrange multipliers can be so useful.
For multiple constraints 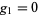 ,
, 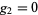 , ...,
, ...,
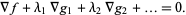 |
(3) |
REFERENCES:
Arfken, G. "Lagrange Multipliers." §17.6 in Mathematical Methods for Physicists, 3rd ed. Orlando, FL: Academic Press, pp. 945-950, 1985.
Lang, S. Calculus of Several Variables. Reading, MA: Addison-Wesley, p. 140, 1973.
Simmons, G. F. Differential Equations. New York: McGraw-Hill, p. 367, 1972.
Zwillinger, D. (Ed.). "Lagrange Multipliers." §5.1.8.1 in CRC Standard Mathematical Tables and Formulae, 31st Ed. Boca Raton, FL: CRC Press, pp. 389-390, 2003.



|
|
|
|
لصحة القلب والأمعاء.. 8 أطعمة لا غنى عنها
|
|
|
|
|
|
|
حل سحري لخلايا البيروفسكايت الشمسية.. يرفع كفاءتها إلى 26%
|
|
|
|
|
|
|
جامعة الكفيل: شراكتنا مع المؤسّسات الرائدة تفتح آفاقًا جديدة للارتقاء بجودة التعليم الطبّي في العراق
|
|
|