

تاريخ الرياضيات

الاعداد و نظريتها

تاريخ التحليل

تار يخ الجبر

الهندسة و التبلوجي


الرياضيات في الحضارات المختلفة

العربية

اليونانية

البابلية

الصينية

المايا

المصرية

الهندية


الرياضيات المتقطعة

المنطق

اسس الرياضيات

فلسفة الرياضيات

مواضيع عامة في المنطق


الجبر

الجبر الخطي

الجبر المجرد

الجبر البولياني

مواضيع عامة في الجبر

الضبابية

نظرية المجموعات

نظرية الزمر

نظرية الحلقات والحقول

نظرية الاعداد

نظرية الفئات

حساب المتجهات

المتتاليات-المتسلسلات

المصفوفات و نظريتها

المثلثات


الهندسة

الهندسة المستوية

الهندسة غير المستوية

مواضيع عامة في الهندسة

التفاضل و التكامل


المعادلات التفاضلية و التكاملية

معادلات تفاضلية

معادلات تكاملية

مواضيع عامة في المعادلات


التحليل

التحليل العددي

التحليل العقدي

التحليل الدالي

مواضيع عامة في التحليل

التحليل الحقيقي

التبلوجيا

نظرية الالعاب

الاحتمالات و الاحصاء

نظرية التحكم

بحوث العمليات

نظرية الكم

الشفرات

الرياضيات التطبيقية

نظريات ومبرهنات


علماء الرياضيات

500AD

500-1499

1000to1499

1500to1599

1600to1649

1650to1699

1700to1749

1750to1779

1780to1799

1800to1819

1820to1829

1830to1839

1840to1849

1850to1859

1860to1864

1865to1869

1870to1874

1875to1879

1880to1884

1885to1889

1890to1894

1895to1899

1900to1904

1905to1909

1910to1914

1915to1919

1920to1924

1925to1929

1930to1939

1940to the present

علماء الرياضيات

الرياضيات في العلوم الاخرى

بحوث و اطاريح جامعية

هل تعلم

طرائق التدريس

الرياضيات العامة

نظرية البيان
Sine-Gordon Equation
المؤلف:
Barone, A.; Esposito, F.; Magee, C. J.; and Scott, A. C
المصدر:
"Theory and Applications of the Sine-Gordon Equation." Riv. Nuovo Cim.1
الجزء والصفحة:
...
23-7-2018
1952
Sine-Gordon Equation
A partial differential equation which appears in differential geometry and relativistic field theory. Its name is a wordplay on its similar form to the Klein-Gordon equation. The equation, as well as several solution techniques, were known in the 19th century, but the equation grew greatly in importance when it was realized that it led to solutions ("kink" and "antikink") with the collisional properties of solitons (Perring and Skyrme 1962; Tabor 1989, p. 307). The sine-Gordon equation also appears in a number of other physical applications (Barone 1971; Gibbon et al. 1979; Bishop and Schneider 1981; Davydov 1985; Infeld and Rowlands 2000, pp. 202 and 240), including the propagation of fluxons in Josephson junctions (a junction between two superconductors), the motion of rigid pendula attached to a stretched wire, and dislocations in crystals.
The sine-Gordon equation is
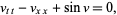 |
(1) |
where 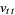 and
and 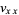 are partial derivatives (Infeld and Rowlands 2000, p. 199).
are partial derivatives (Infeld and Rowlands 2000, p. 199).
The so-called double sine-Gordon equation is given by
![u_(xt)+/-[sinu+etasin(1/2u)]=0](http://mathworld.wolfram.com/images/equations/Sine-GordonEquation/NumberedEquation2.gif) |
(2) |
(Calogero and Degasperis 1982, p. 135; Zwillinger 1995, p. 135).
The equation can be transformed by defining
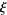 |
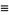 |
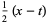 |
(3) |
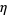 |
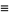 |
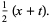 |
(4) |
Then, by the chain rule,
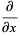 |
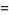 |
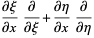 |
(5) |
 |
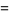 |
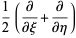 |
(6) |
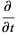 |
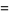 |
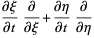 |
(7) |
 |
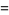 |
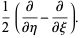 |
(8) |
This gives
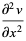 |
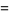 |
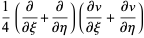 |
(9) |
 |
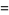 |
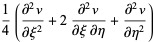 |
(10) |
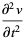 |
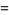 |
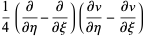 |
(11) |
 |
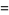 |
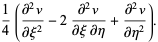 |
(12) |
Plugging in gives
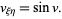 |
(13) |
Another solution to the sine-Gordon equation is given by making the substitution 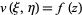 , where
, where 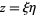 , giving the ordinary differential equation
, giving the ordinary differential equation
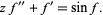 |
(14) |
However, this cannot be solved analytically, since letting 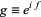 gives
gives
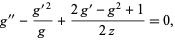 |
(15) |
which is the third Painlevé transcendent (Tabor 1989, p. 309).
While the equation cannot be solved in all generality, several classes of solutions can be found by making the ansatzthat the solution is of of the form
 |
(16) |
This can be physically motivated on the grounds that the identity
 |
(17) |
means that interchanging space and time variables preserves the solution, as required by the symmetry of the sine-Gordon equation (1). (Although the reason for the factor of 4 is not entirely clear.)
Plugging the ansatz (16) into the Sine-Gordon equation (1) then gives
 |
(18) |
(Lamb 1980; Infeld and Rowlands 2000, pp. 199-200, typos corrected). Since the right-hand side contains two terms, one dependent only on 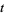 and one only on
and one only on  , it can be eliminated by differentiating both side with respect to both
, it can be eliminated by differentiating both side with respect to both  and
and 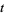 . Doing this and dividing the result by
. Doing this and dividing the result by 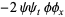 gives
gives
 |
(19) |
which can be written in the slightly simpler form
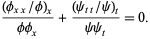 |
(20) |
Since the left term depends on  only and the right term depends on
only and the right term depends on 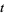 only, separation of variables can be used to write
only, separation of variables can be used to write
 |
(21) |
where the separation constant is assumed to be positive. Rewriting these two equations then gives
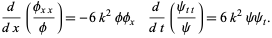 |
(22) |
These can be integrated directly to give
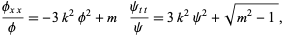 |
(23) |
where 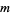 and
and 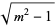 are constants of integration which are connected through equation (◇). Clearing denominators,
are constants of integration which are connected through equation (◇). Clearing denominators,
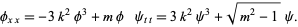 |
(24) |
The final form of the Sine-Gordon equation with the above separation is then
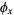 |
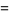 |
 |
(25) |
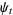 |
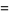 |
 |
(26) |
(Infeld and Rowlands 2000, p. 200, typos corrected), where 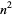 is another constant of integration. These equations can be solved in general in terms of incomplete elliptic integrals of the first kind
is another constant of integration. These equations can be solved in general in terms of incomplete elliptic integrals of the first kind 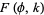 , but interesting classes of solution can be investigated by picking particularly simple values of the integration constants.
, but interesting classes of solution can be investigated by picking particularly simple values of the integration constants.
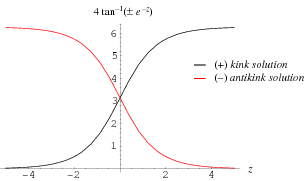
A single-soliton solution is obtained by taking 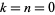 and
and 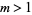 , in which case the equations have the solutions
, in which case the equations have the solutions
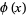 |
 |
 |
(27) |
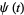 |
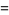 |
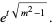 |
(28) |
Plugging into equation (◇) then gives
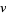 |
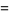 |
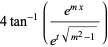 |
(29) |
 |
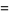 |
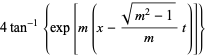 |
(30) |
 |
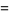 |
 |
(31) |
where 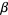 has been defined as
has been defined as
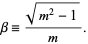 |
(32) |
If 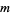 had instead been defined with a minus sign, the same solution but with
had instead been defined with a minus sign, the same solution but with 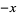 instead of
instead of 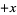 would have been obtained. The positive solution is a soliton also known as the "kink solution," while the negative solution is an antisoliton also known as the "antikink solution" (Tabor 1989, pp. 306-307; Infeld and Rowlands 2000, p. 200).
would have been obtained. The positive solution is a soliton also known as the "kink solution," while the negative solution is an antisoliton also known as the "antikink solution" (Tabor 1989, pp. 306-307; Infeld and Rowlands 2000, p. 200).
A two-soliton solution exists with 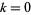 ,
, 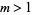 :
:
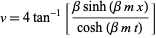 |
(33) |
(Infeld and Rowlands 2000, p. 200).
A two-kink solution is given by
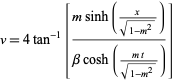 |
(34) |
(Perring and Skyrme 1962; Drazin 1988; Tabor 1989, pp. 307-308).
A "breather" solution occurs for 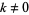 ,
,  ,
, 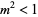 :
:
![v=-4tan^(-1)[m/(sqrt(1-m^2))(sin(sqrt(1-m^2)t))/(cosh(mx))].](http://mathworld.wolfram.com/images/equations/Sine-GordonEquation/NumberedEquation18.gif) |
(35) |
For a fixed 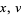 , this is a periodic function of
, this is a periodic function of 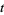 with frequency
with frequency 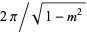 (Infeld and Rowlands 2000, pp. 200-201).
(Infeld and Rowlands 2000, pp. 200-201).
REFERENCES:
Baker, H. F. Abelian Functions: Abel's Theorem and the Allied Theory, Including the Theory of the Theta Functions. New York: Cambridge University Press, p. xix, 1995.
Barone, A.; Esposito, F.; Magee, C. J.; and Scott, A. C. "Theory and Applications of the Sine-Gordon Equation." Riv. Nuovo Cim.1, 227-267, 1971.
Bishop, A. R. and Schneider, T. (Eds.). Solitons and Condensed Matter Physics: Proceedings of a Symposium Held June 19-27, 1978. Berlin: Springer-Verlag, 1981.
Calogero, F. and Degasperis, A. Spectral Transform and Solitons: Tools to Solve and Investigate Nonlinear Evolution Equations.New York: North-Holland, 1982.
Davydov, A. S. Solitons in Molecular Systems. Dordrecht, Netherlands: Reidel, 1985.
Drazin, P. G. and Johnson, R. S. Solitons: An Introduction. Cambridge, England: Cambridge University Press, 1988.
Gibbon, J. D.; James, I. N.; and Moroz, I. M. "The Sine-Gordon Equation as a Model for a Rapidly Rotating Baroclinic Fluid." Phys. Script. 20, 402-408, 1979.
Infeld, E. and Rowlands, G. Nonlinear Waves, Solitons, and Chaos, 2nd ed. Cambridge, England: Cambridge University Press, 2000.
Kaup, D. J. "Method for Solving the Sine-Gordon Equation in Laboratory Coordinates." Stud. Appl. Math. 54, 165-179, 1975.
Lamb, G. L. Jr. Elements of Soliton Theory. New York: Wiley, 1980.
Perring, J. K. and Skyrme, T. H. R. "A Model Unified Field Equation." Nucl. Phys. 31, 550-555, 1962.
Tabor, M. "The Sine-Gordon Equation." §7.5.b in Chaos and Integrability in Nonlinear Dynamics: An Introduction. New York: Wiley, pp. 305-309, 1989.
Zwillinger, D. (Ed.). CRC Standard Mathematical Tables and Formulae. Boca Raton, FL: CRC Press, p. 417, 1995.
 الاكثر قراءة في المعادلات التفاضلية الجزئية
الاكثر قراءة في المعادلات التفاضلية الجزئية
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة

الآخبار الصحية















 قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة
قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة "المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة
"المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة (نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)
(نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)


















