


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 21-5-2018
Date: 23-12-2018
Date: 30-5-2018
|
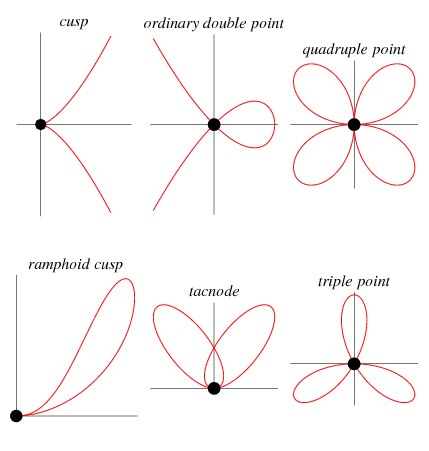
A singular point of an algebraic curve is a point where the curve has "nasty" behavior such as a cusp or a point of self-intersection (when the underlying field 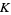 is taken as the reals). More formally, a point
is taken as the reals). More formally, a point 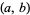 on a curve
on a curve 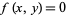 is singular if the
is singular if the  and
and 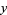 partial derivatives of
partial derivatives of 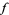 are both zero at the point
are both zero at the point 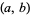 . (If the field
. (If the field 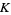 is not the reals or complex numbers, then the partial derivative is computed formally using the usual rules of calculus.)
is not the reals or complex numbers, then the partial derivative is computed formally using the usual rules of calculus.)
The following table gives some representative named curves that have various types of singular points at their origin.
| singularity | curve | equation |
| acnode | 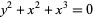 |
|
| cusp | cusp curve | 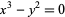 |
| crunode | cardioid | 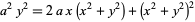 |
| quadruple point | quadrifolium | 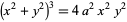 |
| ramphoid cusp | keratoid cusp | 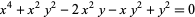 |
| tacnode | capricornoid | 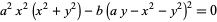 |
| triple point | trifolium | 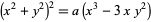 |
Consider the following two examples. For the curve
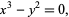 |
the cusp at (0, 0) is a singular point. For the curve
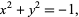 |
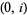 is a nonsingular point and this curve is nonsingular.
is a nonsingular point and this curve is nonsingular.
Singular points are sometimes known as singularities, and vice versa.
REFERENCES:
Arfken, G. "Singularities" and "Singular Points." §7.1 and 8.4 in Mathematical Methods for Physicists, 3rd ed. Orlando, FL: Academic Press, pp. 396-400 and 451-454, 1985.



|
|
|
|
علامات بسيطة في جسدك قد تنذر بمرض "قاتل"
|
|
|
|
|
|
|
أول صور ثلاثية الأبعاد للغدة الزعترية البشرية
|
|
|
|
|
|
|
مستشفى العتبة العباسية الميداني في سوريا يقدّم خدماته لنحو 1500 نازح لبناني يوميًا
|
|
|