
تاريخ الفيزياء

علماء الفيزياء


الفيزياء الكلاسيكية

الميكانيك

الديناميكا الحرارية


الكهربائية والمغناطيسية

الكهربائية

المغناطيسية

الكهرومغناطيسية


علم البصريات

تاريخ علم البصريات

الضوء

مواضيع عامة في علم البصريات

الصوت


الفيزياء الحديثة


النظرية النسبية

النظرية النسبية الخاصة

النظرية النسبية العامة

مواضيع عامة في النظرية النسبية

ميكانيكا الكم

الفيزياء الذرية

الفيزياء الجزيئية


الفيزياء النووية

مواضيع عامة في الفيزياء النووية

النشاط الاشعاعي


فيزياء الحالة الصلبة

الموصلات

أشباه الموصلات

العوازل

مواضيع عامة في الفيزياء الصلبة

فيزياء الجوامد


الليزر

أنواع الليزر

بعض تطبيقات الليزر

مواضيع عامة في الليزر


علم الفلك

تاريخ وعلماء علم الفلك

الثقوب السوداء


المجموعة الشمسية

الشمس

كوكب عطارد

كوكب الزهرة

كوكب الأرض

كوكب المريخ

كوكب المشتري

كوكب زحل

كوكب أورانوس

كوكب نبتون

كوكب بلوتو

القمر

كواكب ومواضيع اخرى

مواضيع عامة في علم الفلك

النجوم

البلازما

الألكترونيات

خواص المادة


الطاقة البديلة

الطاقة الشمسية

مواضيع عامة في الطاقة البديلة

المد والجزر

فيزياء الجسيمات


الفيزياء والعلوم الأخرى

الفيزياء الكيميائية

الفيزياء الرياضية

الفيزياء الحيوية

الفيزياء العامة


مواضيع عامة في الفيزياء

تجارب فيزيائية

مصطلحات وتعاريف فيزيائية

وحدات القياس الفيزيائية

طرائف الفيزياء

مواضيع اخرى
تعريف كمي للقوة، علم استاتيكا الجسيمات
المؤلف:
مايكل كوهين
المصدر:
الميكانيكا الكلاسيكية مقدمة أساسية
الجزء والصفحة:
ص 46 – ص 48
2024-09-05
522
ينص قانون نيوتن الثاني على أن عجلة أي جسم تتناسب طرديا مع القوة الكلية المؤثرة على هذا الجسم. يستخدم بعض المؤلفين هذه الحقيقة أساسًا لتعريف كمي للقوة. سوف نطرح تعريف «القوة» كَميًّا قبل مناقشة القانون الثاني. وبذلك سيكون من الواضح أن القانون الثاني تقرير عن الكون، وليس مجرد تعريف لكلمة «قوة». وسوف نعتاد عندئذٍ على تحليل القوى عن طريق دراسة عدد من أمثلة الاتزان الاستاتيكي للجسيمات.
بالنسبة إلى وحدة القوة اخترنا حالة الدفع أو الشد البسيطة التي يسهل تكرارها. وهذا ينتج، على سبيل المثال، من زنبرك معياري ممدود بكَمِّيَّة معيارية عند درجة حرارة معيارية. وتكون وحدتا القوة إذن هما القوة المؤثرة بواسطة اثنين من تلك الزنبركات المعيارية، مربوطين بالجسم ذاته ويشدانه في نفس الاتجاه. (حسب خواص الزنبرك، قد يكون هذا مماثلا للقوة التي يؤثر بها زنبرك وحيد ممدود بضعف الكمية المعيارية أو لا يكون كذلك.)
الأكثر غرابة من ذلك، إذا تخيَّلنا أن لدينا مصدرًا لفئران متماثلة، تشد دائما بكامل قوتها، يمكن إذن استخدام «الفأر» وحدة للقوة. يمكن تمثيل فأر واحد يشد في اتجاه معين بواسطة سهم طوله وحدة واحدة يشير في ذلك الاتجاه. ويمكن تمثيل ثلاثة فئران تجذب في نفس الاتجاه بسهم طوله ثلاث وحدات يشير في ذلك الاتجاه. يمكن تعميم التعريف بسهولة على أعداد كسرية من الفئران؛ فمثلا إذا وجد أن سبعة سناجب تشد في اتجاه معين، تصنع بالضبط نفس تأثير تسعة عشر فأرًا تشد في ذلك الاتجاه، فإننا عندئذ نمثل القوة التي يؤثر بها سنجاب واحد بسهم طوله 19/7 في الاتجاه الملائم. (بما أن أي عدد صحيح هو نهاية متوالية من الأعداد الكسرية؛ فإن التعريف مُعمَّم بسهولة على القوى التي تكافئ عددًا صحيحًا من الفئران. (وهو ليس مثل عدد من الفئران الصحيحة!)) وهكذا يمكن تمثيل أي دفع أو شد في اتجاه محدد بسهم في ذلك الاتجاه، ويكون طول السهم هو عدد الفئران اللازم لكي يحاكي بإتقان الدفع أو الشد المعطى.
بما أننا أنشأنا طريقة لتمثيل القوى بواسطة أسهم لها أطوال واتجاهات، فيبدو من البدهي تقريبًا أن القوى لها جميع خصائص المتجهات. وبالأخص عند افتراض وجود فريقين من الفئران مربوطين بنفس النقطة على نفس الجسم. ليكن أحد الفريقين متكونا من N1 فأرًا تشد جميعها في نفس الاتجاه (ممثلًا بمتجه 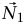 )، وليكن الفريق الآخر متكونًا من N2 فأرًا تشدُّ جميعها في اتجاه آخر (ممثلًا بمتجه
)، وليكن الفريق الآخر متكونًا من N2 فأرًا تشدُّ جميعها في اتجاه آخر (ممثلًا بمتجه  ). أليس من الواضح أن فريقي الفئران اللذين يشدان بالتزامن يكافئان من جميع النواحي فريقًا واحدًا من الفئران حيث يكون اتجاه هذا الفريق الوحيد هو اتجاه المتجه
). أليس من الواضح أن فريقي الفئران اللذين يشدان بالتزامن يكافئان من جميع النواحي فريقًا واحدًا من الفئران حيث يكون اتجاه هذا الفريق الوحيد هو اتجاه المتجه 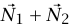 ويكون عدد الفئران في الفريق الوحيد |
ويكون عدد الفئران في الفريق الوحيد | |؛ أي طول المتجه
|؛ أي طول المتجه  ؟ أعتقد أن لدينا هنا نقطة مهمة تحتاج إلى برهان ويمكن برهنتها دون الاستعانة بتجربة.
؟ أعتقد أن لدينا هنا نقطة مهمة تحتاج إلى برهان ويمكن برهنتها دون الاستعانة بتجربة.
على أي حال، ينبغي أن نعي بوضوح أنه عندما نُمَثْل القوى بمتجهات، فإننا لا نعني فقط أن للقوة مقدارًا واتجاهًا، وإنما نعني أيضًا أن «أي قوتين (كلٌّ منهما يمثلها متجه) تؤثران بالتزامن على نفس النقطة تكافئان قوة واحدة، مُمَثَّلة بمتح حاصل جمع متجهي هاتين القوتين.» ينتج من ذلك أن تأثير أكثر من قوتين على نفس النقطة، يكافئ تأثير قوة واحدة مُمَثْلة بمتجه حاصل جمع المتجهات التي تمثل القوى المنفردة.
يمكننا الآن مناقشة اتِّزان الكتل النقطية. و«الكتلة النُّقَطيَّة» هي جسم صغير جدا لدرجة تجعلنا نقيس فقط موضعه مع إهمال حقيقة أن أجزاء الجسم المختلفة قد تكون لها سرعات مختلفة. سنرى حالا – نتيجة لقانون نيوتن الثالث – أن قوانين نيوتن لا تُطَبَّق فقط على الكتل النقطية ولكن تُطَبَّق أيضًا على أجسام مركبة أكبر حجمًا تتكون من عدة كتل نقطية.
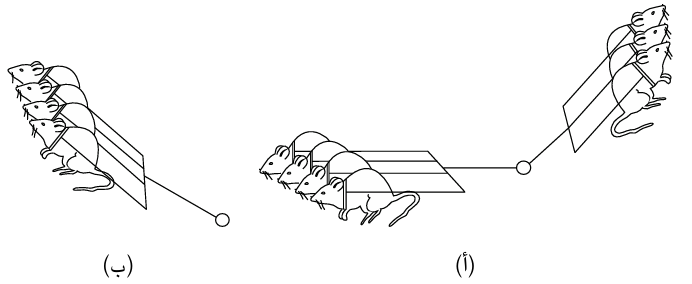
شكل 2–1: فريقان من الفئران مربوطان بنفس النقطة على نفس الجسم (شكل (أ) بالأعلى). يتكون أحد الفريقين من N1 فأرًا تشد في نفس الاتجاه الذي يمثله المتجه 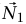 ويتكون الفريق الآخر N2 من فأرًا تشد في نفس الاتجاه الذي يمثله المتجه
ويتكون الفريق الآخر N2 من فأرًا تشد في نفس الاتجاه الذي يمثله المتجه 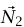 . أليس من الواضح أن فريقي الفئران مكافئان لفريق واحد (شكل (ب))؛ حيث يكون اتجاه الفريق الوحيد هو اتجاه المتجه
. أليس من الواضح أن فريقي الفئران مكافئان لفريق واحد (شكل (ب))؛ حيث يكون اتجاه الفريق الوحيد هو اتجاه المتجه 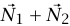 وعدد الفئران في الفريق الوحيد هو مقدار المتجه
وعدد الفئران في الفريق الوحيد هو مقدار المتجه 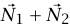 ؟ للبرهان، انظر ملحق (ج).
؟ للبرهان، انظر ملحق (ج).
يقال إن جسمًا ما في حالة اتزان عندما يكون ساكنًا (ليس فقط للحظة، ولكن بصورة مستديمة أو على الأقل لفترة زمنية محددة؛ فإذا رميت كرة رأسيًا لأعلى، فسوف تكون ساكنة لحظيًّا في اللحظة التي تصل عندها إلى أعلى نقطة. الكرة لا تكون في حالة اتزان عند تلك اللحظة؛ لأنها لا تبقى ثابتة لفترة زمنية محددة، كما أن القوة المحصلة المؤثرة على الكرة ليست صفرًا من ناحية أخرى، الكرة المستقرة على الأرض تكون في حالة اتزان.) أو متحركا بسرعة ثابتة. طبقًا لقانون نيوتن الأول، الجسم وهو في حالة اتزان لا تؤثر عليه قوة.
أبسط مثال للاتزان هو جسيم خارج مجال المجموعة الشمسية، يبعد بدرجة كافية عن الشمس والكواكب بحيث يكون من الممكن إهمال قوى الجاذبية التي يتعرض لها. هذا المثال لا يثير الاهتمام نظرًا لعدم وجود قُوًى مؤثرة على الجسيم. أمثلة الاتزان الأكثر أهمية – وهي ما نصادفها في حياتنا اليومية – هي تلك الحالات التي يكون فيها صافي (أو «محصلة») القوة على جسم صفرا، رغم وجود عدة قوى مؤثرة على الجسم؛ لذلك فإن اتزان الجسم ينتج من حقيقة أن المجموع المتجهي لجميع القوى المؤثرة على الجسم يكون صفرًا.