تُنشئ الطريقة الهندسية المتجه 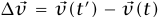 بشكل صريح وتحسب النهاية المطلوبة بواسطة المعادلة (16–1). نجعل t' = t + Δt ونبين في شكل 1–10 موضع ومتجه سرعة الجسيم عند زمن t وزمن tΔt+. الصورة مرسومة لجسيم يتحرك باتجاه عكس عقارب الساعة، ولكننا سوف نرى أن العجلة نفسها تحدث عند الحركة باتجاه عقارب الساعة. لاحظ أن المتجهين  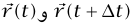لهما نفس الطول r، وأن المتجهين 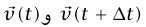لهما نفس الطول v لافتراض أن مقدار السرعة ثابت. الأكثر من ذلك، الزاوية بين المتجهين ذاتها الزاوية بين المتجهي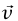ن لأن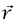 عمودي على  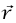عند كل لحظة. يكون طول القوس المقطوع بواسطة الجسيم خلال زمن tΔ هو tΔv، والقياس الدائري للزاوية بين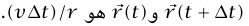

نحن مهتمون بالنهاية 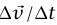 عندما تئول 0 → tΔ. إذا قمنا بجلب ذيلي  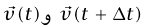معا عن طريق إزاحة متوازية لأي من المتجهين يكون عندئذ  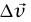هو المتجه من قمة  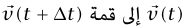(انظر شكل 1–11). المثلث في شكل 1–11 متساوي الساقين، وعندما تئول 0 → tΔ تصبح زاويتا قاعدة المثلث متساوي الساقين قائمتين. لذلك نرى أن  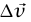تصبح عمودية على متجه السرعة اللحظية  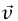وتوازي  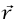في الاتجاه العكسي (يكون هذا صحيحًا أيضًا للحركة في اتجاه عقارب الساعة وهو ما يمكن تبينه من رسم الصورة).

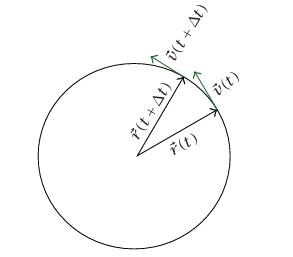
شکل 1–10: هندسة إنشاء العجلة لحركة دائرية ذات مقدار سرعة ثابت.

وبما أن المثلثين متساويي الساقين في شكلي 1–11 و1–12 متشابهان، فإن 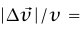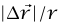. وحيث إن الزاوية بين  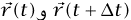صغيرة جدًّا، فيمكن الاستعاضة عن طول الوتر  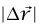بطول القوس tΔv. وبهذا .

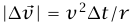لقد بيّنا إذن أن متجه العجلة له المقدار r/v² واتجاهه يكون من الموضع اللحظي للجسيم ناحية مركز الدائرة، أي:

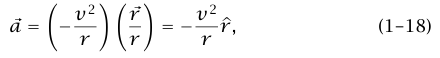
حيث 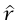هو متجه وحدة يشير من مركز الدائرة ناحية الجسيم. تسمى هذه العجلة التي قمنا بحسابها عادة بالعجلة المركزية كلمة «مركزية» تعني أنها «متجهة ناحية المركز» وهي لمجرد التذكير باتجاه 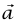. إذا لم يكن مقدار السرعة v ثابتًا، يكون للعجلة مركبة مماسية أيضًا مقدارها dv/dt.

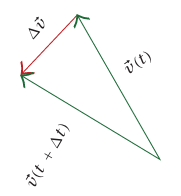
شكل 1–11: إنشاء هندسي لتغير السرعة لحركة دائرية ذات مقدار سرعة ثابت.

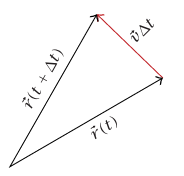
شكل 1–12: إنشاء هندسي لتغير الموضع لحركة دائرية ذات مقدار سرعة ثابت.

مواضيع ذات صلة

أنظمة لأكثر من جسيم واحد

كمية التحرك الزاوية والقوة المركزية

الحركة الدورانية

امثلة عن الاتزان الاستاتيكي للأجسام الممتدة

الاتزان الاستاتيكي للأجسام الممتدة

تعريف العزم

تذبذبات صغيرة لبندول

اعتبارات الطاقة في الحركة التوافقية البسيطة

الحل الهندسي للمعادلة التفاضلية للحركة التوافقية البسيطة، دائرة المرجع

الحل باستخدام حساب التفاضل والتكامل

قانون هوك والمعادلة التفاضلية للحركة التوافقية البسيطة

القدرة ووحدات الشغل