حساب الكمون الناتج عن مجموعة الشحن في M
المؤلف:
الدكتور محمد انور بطل
المصدر:
الفيزياء الذرية والجزيئية
الجزء والصفحة:
ص 220
11-2-2022
2262
حساب الكمون الناتج عن مجموعة الشحن في M
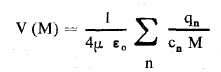
ولحساب M 1/cn نقوم بنشر محدود بالنسبة للكميات الصغيرة جداً xn, yn, zn:
إذاً :
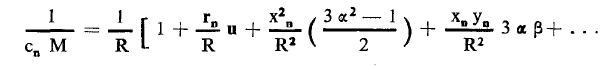
بإضافة مساهمات كل الشحن نحصل على :
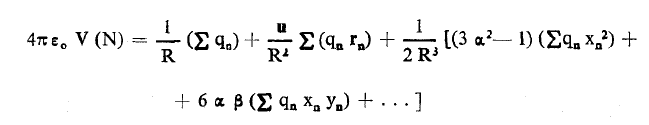
ولتفسير هذه النتيجة نجد:
a) - في الحالة التي يكون فيها qn ≠ 0 ∑ يوجد barycentre للشحن qn ويمكن أن نضع في هذه النقطة المركز c؛ بينما qn rn = 0 ∑ والحدود من المرتبة الثانية ستنعدم. الحد الأول بعد الحد R1 يكون tern ب 1R3 (حالة خاصة لأنوية الذرات).
b) - في الحالة التي يكون فيها qn = 0 ∑ فان المجموع qn rn ∑ مستقل عن المبدأ c ندعو بعزم ثنائي القطب الكهربائي المتجهة p =∑ qn rn لأن الشكل الأبسط لتحقيق مثل هذه المجموعة من الشحن هو اختبار شحنتان متساويتان لكن بأشارتين متعاكستين.
(من الممكن اختبار المبدأ وتوجيه المحاور بحيث ينعدم الحد R31).
c) - في الحالة التي يكون فيها qn = 0 ∑ و qn rn ∑ بنفس الوقت ، لم تعد الحدود الأولى معدوم ومن السهل بيان بأن معاملات الحدود السته مستقلة عن المبدأ المختار c ندعو بعزم رباعي الأقطاب الكهربائي التنسور المتناظر من المرتبة الثانية المشكل من هذه المعاملات الستة qn xn yn , ∑ qn xn2 ∑ لأن أبسط طريقة يحقق بها هو اختبار أربع شحن متساوية بالطويلة موضوعة على رأس متوازي أضلاع بشكل تشكل فيه ثنائيات قطب متعاكسة. كما في الشكل (1).
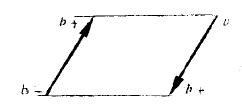
الشكل (1)
d) - بشكل عام ندعو بعزم متعدد الأقطاب الكهربائي من الرتبة 2n مجموعة المعاملات التي تسمح بالتعبير عن الحد 1 Rn+1 ،لأن أبسط طريقة لعدم مجموعة الحدود السابقة هو اختبار مجموعة ل 2n شحنة متعاكسة .
الاكثر قراءة في الفيزياء الذرية
اخر الاخبار
اخبار العتبة العباسية المقدسة
