Erfc
المؤلف:
Abramowitz, M. and Stegun, I. A.
المصدر:
"Repeated Integrals of the Error Function." §7.2 in Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover
الجزء والصفحة:
...
18-11-2018
2755
Erfc
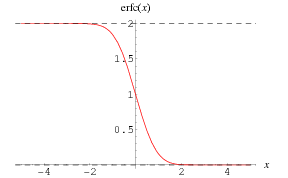
Erfc is the complementary error function, commonly denoted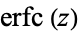 
, is an entire function defined by
It is implemented in the Wolfram Language as Erfc[z].
Note that some authors (e.g., Whittaker and Watson 1990, p. 341) define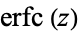 
without the leading factor of 
.
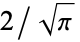For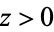 
,
 |
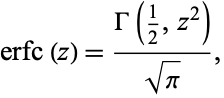(3)
|
where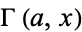 
is the incomplete gamma function.
The derivative is given by
 |
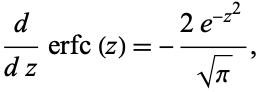(4)
|
and the indefinite integral by
 |
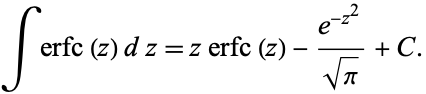(5)
|
It has the special values
It satisfies the identity
 |
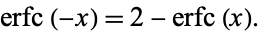(9)
|
It has definite integrals
For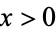 
, 
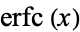is bounded by
 |
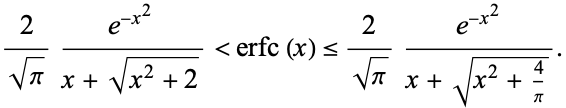(13)
|
Erfc can also be extended to the complex plane, as illustrated above.
A generalization is obtained from the erfc differential equation
 |
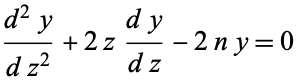(14)
|
(Abramowitz and Stegun 1972, p. 299; Zwillinger 1997, p. 122). The general solution is then
 |
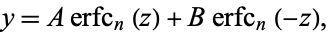(15)
|
where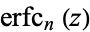 
is the repeated erfc integral. For integer 
,
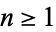(Abramowitz and Stegun 1972, p. 299), where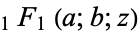 
is a confluent hypergeometric function of the first kind and 
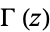is a gamma function. The first few values, extended by the definition for 
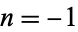and 0, are given by
REFERENCES:
Abramowitz, M. and Stegun, I. A. (Eds.). "Repeated Integrals of the Error Function." §7.2 in Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, pp. 299-300, 1972.
Arfken, G. Mathematical Methods for Physicists, 3rd ed. Orlando, FL: Academic Press, pp. 568-569, 1985.
Press, W. H.; Flannery, B. P.; Teukolsky, S. A.; and Vetterling, W. T. "Incomplete Gamma Function, Error Function, Chi-Square Probability Function, Cumulative Poisson Function." §6.2 in Numerical Recipes in FORTRAN: The Art of Scientific Computing, 2nd ed. Cambridge, England: Cambridge University Press, pp. 209-214, 1992.
Spanier, J. and Oldham, K. B. "The Error Function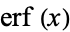 
and Its Complement 
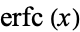" and "The 
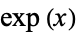and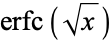 
and Related Functions." Chs. 40 and 41 in An Atlas of Functions. Washington, DC: Hemisphere, pp. 385-393 and 395-403, 1987.
Whittaker, E. T. and Watson, G. N. A Course in Modern Analysis, 4th ed. Cambridge, England: Cambridge University Press, 1990.
Zwillinger, D. Handbook of Differential Equations, 3rd ed. Boston, MA: Academic Press, p. 122, 1997.
الاكثر قراءة في التحليل العقدي
اخر الاخبار
اخبار العتبة العباسية المقدسة
