

تاريخ الرياضيات

الاعداد و نظريتها

تاريخ التحليل

تار يخ الجبر

الهندسة و التبلوجي


الرياضيات في الحضارات المختلفة

العربية

اليونانية

البابلية

الصينية

المايا

المصرية

الهندية


الرياضيات المتقطعة

المنطق

اسس الرياضيات

فلسفة الرياضيات

مواضيع عامة في المنطق


الجبر

الجبر الخطي

الجبر المجرد

الجبر البولياني

مواضيع عامة في الجبر

الضبابية

نظرية المجموعات

نظرية الزمر

نظرية الحلقات والحقول

نظرية الاعداد

نظرية الفئات

حساب المتجهات

المتتاليات-المتسلسلات

المصفوفات و نظريتها

المثلثات


الهندسة

الهندسة المستوية

الهندسة غير المستوية

مواضيع عامة في الهندسة

التفاضل و التكامل


المعادلات التفاضلية و التكاملية

معادلات تفاضلية

معادلات تكاملية

مواضيع عامة في المعادلات


التحليل

التحليل العددي

التحليل العقدي

التحليل الدالي

مواضيع عامة في التحليل

التحليل الحقيقي

التبلوجيا

نظرية الالعاب

الاحتمالات و الاحصاء

نظرية التحكم

بحوث العمليات

نظرية الكم

الشفرات

الرياضيات التطبيقية

نظريات ومبرهنات


علماء الرياضيات

500AD

500-1499

1000to1499

1500to1599

1600to1649

1650to1699

1700to1749

1750to1779

1780to1799

1800to1819

1820to1829

1830to1839

1840to1849

1850to1859

1860to1864

1865to1869

1870to1874

1875to1879

1880to1884

1885to1889

1890to1894

1895to1899

1900to1904

1905to1909

1910to1914

1915to1919

1920to1924

1925to1929

1930to1939

1940to the present

علماء الرياضيات

الرياضيات في العلوم الاخرى

بحوث و اطاريح جامعية

هل تعلم

طرائق التدريس

الرياضيات العامة

نظرية البيان
Erf
المؤلف:
Abramowitz, M. and Stegun, I. A.
المصدر:
"Error Function and Fresnel Integrals." Ch. 7 in Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover
الجزء والصفحة:
...
18-11-2018
2869
Erf
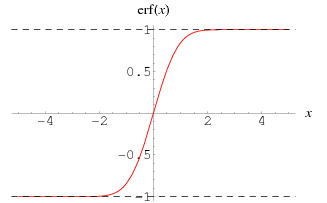
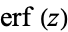 is the "error function" encountered in integrating the normal distribution (which is a normalized form of the Gaussian function). It is an entire functiondefined by
is the "error function" encountered in integrating the normal distribution (which is a normalized form of the Gaussian function). It is an entire functiondefined by
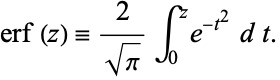 |
(1) |
Note that some authors (e.g., Whittaker and Watson 1990, p. 341) define  without the leading factor of
without the leading factor of 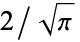 .
.
Erf is implemented in the Wolfram Language as Erf[z]. A two-argument form giving 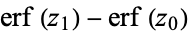 is also implemented as Erf[z0, z1].
is also implemented as Erf[z0, z1].
Erf satisfies the identities
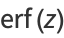 |
 |
 |
(2) |
 |
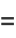 |
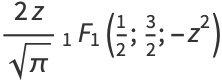 |
(3) |
 |
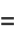 |
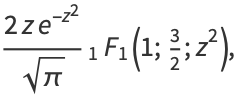 |
(4) |
where 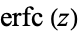 is erfc, the complementary error function, and
is erfc, the complementary error function, and 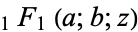 is a confluent hypergeometric function of the first kind. For
is a confluent hypergeometric function of the first kind. For 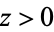 ,
,
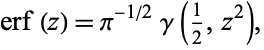 |
(5) |
where 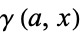 is the incomplete gamma function.
is the incomplete gamma function.
Erf can also be defined as a Maclaurin series
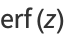 |
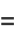 |
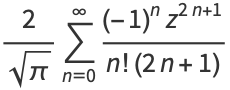 |
(6) |
 |
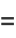 |
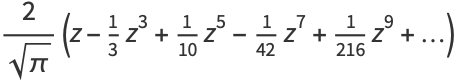 |
(7) |
(OEIS A007680). Similarly,
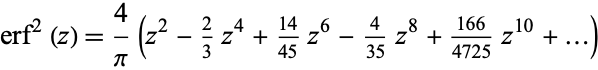 |
(8) |
(OEIS A103979 and A103980).
For 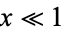 ,
, 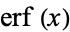 may be computed from
may be computed from
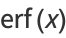 |
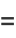 |
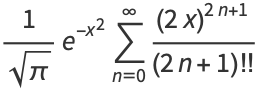 |
(9) |
 |
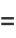 |
![2/(sqrt(pi))e^(-x^2)[x+(2x^3)/(1·3)+(4x^5)/(1·3·5)+...]](http://mathworld.wolfram.com/images/equations/Erf/Inline31.gif) |
(10) |
(OEIS A000079 and A001147; Acton 1990).
For 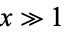 ,
,
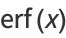 |
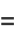 |
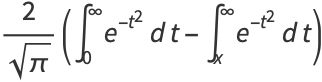 |
(11) |
 |
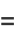 |
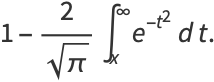 |
(12) |
Using integration by parts gives
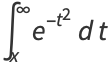 |
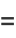 |
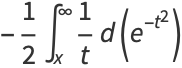 |
(13) |
 |
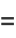 |
![-1/2[(e^(-t^2))/t]_x^infty-1/2int_x^infty(e^(-t^2)dt)/(t^2)](http://mathworld.wolfram.com/images/equations/Erf/Inline44.gif) |
(14) |
 |
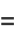 |
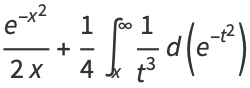 |
(15) |
 |
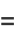 |
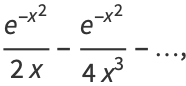 |
(16) |
so
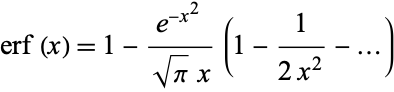 |
(17) |
and continuing the procedure gives the asymptotic series
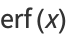 |
 |
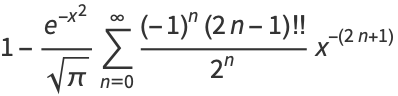 |
(18) |
 |
 |
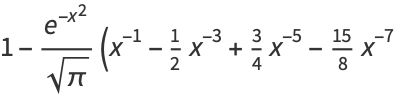 |
(19) |
 |
 |
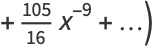 |
(20) |
(OEIS A001147 and A000079).
Erf has the values
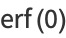 |
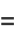 |
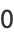 |
(21) |
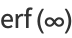 |
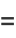 |
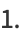 |
(22) |
It is an odd function
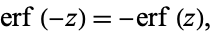 |
(23) |
and satisfies
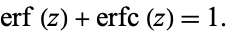 |
(24) |
Erf may be expressed in terms of a confluent hypergeometric function of the first kind 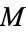 as
as
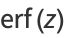 |
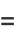 |
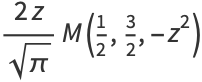 |
(25) |
 |
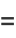 |
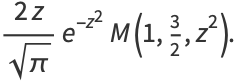 |
(26) |
Its derivative is
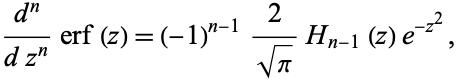 |
(27) |
where 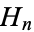 is a Hermite polynomial. The first derivative is
is a Hermite polynomial. The first derivative is
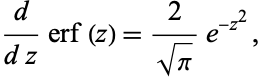 |
(28) |
and the integral is
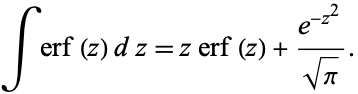 |
(29) |
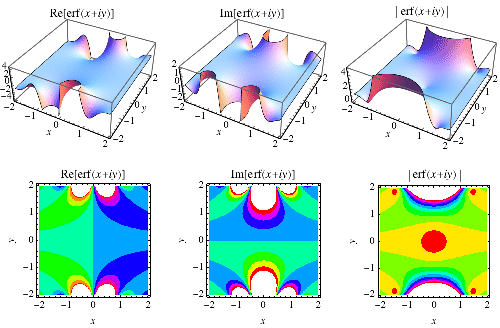 |
Erf can also be extended to the complex plane, as illustrated above.
A simple integral involving erf that Wolfram Language cannot do is given by
![int_0^pe^(-x^2)erf(p-x)dx=1/2sqrt(pi)[erf(1/2sqrt(2)p)]^2](http://mathworld.wolfram.com/images/equations/Erf/NumberedEquation10.gif) |
(30) |
(M. R. D'Orsogna, pers. comm., May 9, 2004). More complicated integrals include
![int_0^infty(e^(-(p+x)y))/(pi(p+x))sin(asqrt(x))dx=-sinh(asqrt(p))
+(e^(-asqrt(p)))/2erf(a/(2sqrt(y))-sqrt(py))+(e^(asqrt(p)))/2erf(a/(2sqrt(y))+sqrt(py))
int_0^infty(sqrt(x)e^(-(p+x)y))/(pi(p+x))cos(asqrt(x))dx=(e^(-[py+a^2/(4y)]))/(sqrt(piy))+sqrt(p)[-cosh(asqrt(p))-(e^(-asqrt(p)))/2erf(a/(2sqrt(y))-sqrt(py))+(e^(asqrt(p)))/2erf(a/(2sqrt(y))+sqrt(py))]](http://mathworld.wolfram.com/images/equations/Erf/NumberedEquation11.gif) |
(31) |
(M. R. D'Orsogna, pers. comm., Dec. 15, 2005).
Erf has the continued fraction
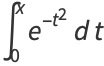 |
 |
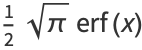 |
(32) |
 |
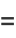 |
 |
(33) |
(Wall 1948, p. 357), first stated by Laplace in 1805 and Legendre in 1826 (Olds 1963, p. 139), proved by Jacobi, and rediscovered by Ramanujan (Watson 1928; Hardy 1999, pp. 8-9).
Definite integrals involving 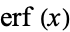 include Definite integrals involving
include Definite integrals involving 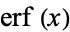 include
include
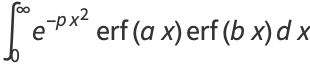 |
 |
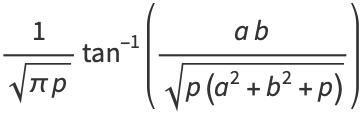 |
(34) |
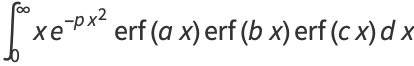 |
 |
![1/(pip)[a/(sqrt(a^2+p))tan^(-1)((bc)/(sqrt((a^2+b^2+c^2+p)(a^2+p))))+b/(sqrt(b^2+p))tan^(-1)((ac)/(sqrt((a^2+b^2+c^2+p)(b^2+p))))+c/(sqrt(c^2+p))tan^(-1)((ab)/(sqrt((a^2+b^2+c^2+p)(c^2+p))))]](http://mathworld.wolfram.com/images/equations/Erf/Inline87.gif) |
(35) |
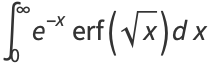 |
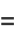 |
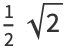 |
(36) |
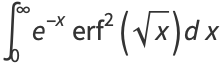 |
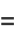 |
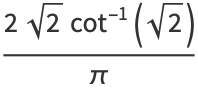 |
(37) |
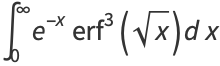 |
 |
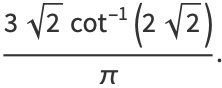 |
(38) |
The first two of these appear in Prudnikov et al. (1990, p. 123, eqns. 2.8.19.8 and 2.8.19.11), with ![R[p]>0](http://mathworld.wolfram.com/images/equations/Erf/Inline97.gif) ,
, 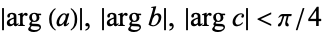 .
.
A complex generalization of 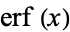 is defined as
is defined as
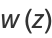 |
 |
 |
(39) |
 |
 |
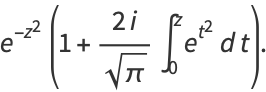 |
(40) |
Integral representations valid only in the upper half-plane ![I[z]>0](http://mathworld.wolfram.com/images/equations/Erf/Inline106.gif) are given by
are given by
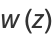 |
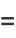 |
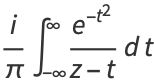 |
(41) |
 |
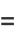 |
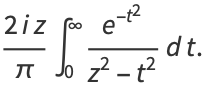 |
(42) |
REFERENCES:
Abramowitz, M. and Stegun, I. A. (Eds.). "Error Function and Fresnel Integrals." Ch. 7 in Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, pp. 297-309, 1972.
Acton, F. S. Numerical Methods That Work, 2nd printing. Washington, DC: Math. Assoc. Amer., p. 16, 1990.
Arfken, G. Mathematical Methods for Physicists, 3rd ed. Orlando, FL: Academic Press, pp. 568-569, 1985.
Hardy, G. H. Ramanujan: Twelve Lectures on Subjects Suggested by His Life and Work, 3rd ed. New York: Chelsea, 1999.
Havil, J. Gamma: Exploring Euler's Constant. Princeton, NJ: Princeton University Press, p. 105, 2003.
Olds, C. D. Continued Fractions. New York: Random House, 1963.
Prudnikov, A. P.; Brychkov, Yu. A.; and Marichev, O. I. Integrals and Series, Vol. 2: Special Functions. New York: Gordon and Breach, 1990.
Sloane, N. J. A. Sequences A000079/M1129, A001147/M3002, A007680/M2861, A103979, A103980 in "The On-Line Encyclopedia of Integer Sequences."
Spanier, J. and Oldham, K. B. "The Error Function 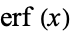 and Its Complement
and Its Complement 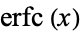 ." Ch. 40 in An Atlas of Functions. Washington, DC: Hemisphere, pp. 385-393, 1987.
." Ch. 40 in An Atlas of Functions. Washington, DC: Hemisphere, pp. 385-393, 1987.
Wall, H. S. Analytic Theory of Continued Fractions. New York: Chelsea, 1948.
Watson, G. N. "Theorems Stated by Ramanujan (IV): Theorems on Approximate Integration and Summation of Series." J. London Math. Soc. 3, 282-289, 1928.
Whittaker, E. T. and Robinson, G. "The Error Function." §92 in The Calculus of Observations: A Treatise on Numerical Mathematics, 4th ed. New York: Dover, pp. 179-182, 1967.
Whittaker, E. T. and Watson, G. N. A Course in Modern Analysis, 4th ed. Cambridge, England: Cambridge University Press, 1990.
 الاكثر قراءة في التحليل العقدي
الاكثر قراءة في التحليل العقدي
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة

الآخبار الصحية















 قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة
قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة "المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة
"المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة (نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)
(نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)


















