Complex Residue
المؤلف:
المرجع الالكتروني للمعلوماتيه
المصدر:
المرجع الالكتروني للمعلوماتيه
الجزء والصفحة:
...
18-12-2018
1664
Complex Residue
The constant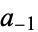 
in the Laurent series
 |
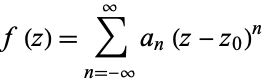(1)
|
of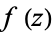 
about a point 
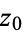is called the residue of 
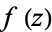. If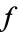 
is analytic at 
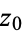, its residue is zero, but the converse is not always true (for example, 
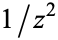has residue of 0 at 
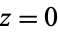but is not analytic at 
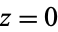). The residue of a function 
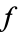at a point 
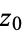may be denoted 
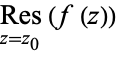. The residue is implemented in the Wolfram Language as Residue[f, ![<span style=]()
{" src="http://mathworld.wolfram.com/images/equations/ComplexResidue/Inline13.gif" style="height:14px; width:5px" />z, z0![<span style=]()
}" src="http://mathworld.wolfram.com/images/equations/ComplexResidue/Inline14.gif" style="height:14px; width:5px" />].
Two basic examples of residues are given by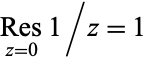 
and 
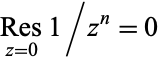for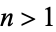 
.
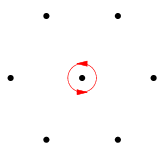
The residue of a function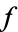 
around a point 
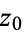is also defined by
 |
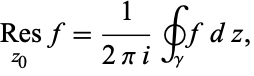(2)
|
where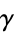 
is counterclockwise simple closed contour, small enough to avoid any other poles of 
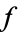. In fact, any counterclockwise path with contour winding number 1 which does not contain any other poles gives the same result by the Cauchy integral formula. The above diagram shows a suitable contour for which to define the residue of function, where the poles are indicated as black dots.
It is more natural to consider the residue of a meromorphic one-form because it is independent of the choice of coordinate. On a Riemann surface, the residue is defined for a meromorphic one-form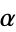 
at a point 
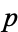by writing 
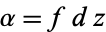in a coordinate 
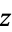around 
. Then
 |
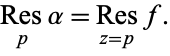(3)
|
The sum of the residues of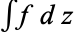 
is zero on the Riemann sphere. More generally, the sum of the residues of a meromorphic one-form on a compact Riemann surface must be zero.
The residues of a function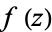 
may be found without explicitly expanding into a Laurent series as follows. If 
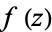has a pole of order 
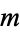at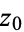 
, then 
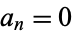for 
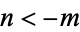and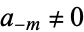 
. Therefore,
 |
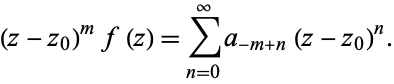(4)
|
Iterating,
![(d^(m-1))/(dz^(m-1))[(z-z_0)^mf(z)]=sum_(n=0)^infty(n+1)(n+2)...(n+m-1)a_(n-1)(z-z_0)^n
=(m-1)!a_(-1)+sum_(n=1)^infty(n+1)(n+2)...(n+m-1)a_(n-1)(z-z_0)^(n-1).](http://mathworld.wolfram.com/images/equations/ComplexResidue/NumberedEquation5.gif) |
(12)
|
So
and the residue is
![a_(-1)=1/((m-1)!)(d^(m-1))/(dz^(m-1))[(z-z_0)^mf(z)]_(z=z_0).](http://mathworld.wolfram.com/images/equations/ComplexResidue/NumberedEquation6.gif) |
(15)
|
The residues of a holomorphic function at its poles characterize a great deal of the structure of a function, appearing for example in the amazing residue theorem of contour integration.
الاكثر قراءة في التحليل العقدي
اخر الاخبار
اخبار العتبة العباسية المقدسة
