Laplace,s Equation--Toroidal Coordinates
المؤلف:
Morse, P. M. and Feshbach, H
المصدر:
Methods of Theoretical Physics, Part I. New York: McGraw-Hill
الجزء والصفحة:
...
21-7-2018
2280
Laplace's Equation--Toroidal Coordinates
In toroidal coordinates, Laplace's equation becomes
 |
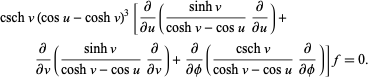(1)
|
Attempt separation of variables by plugging in the trial solution
 |
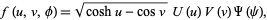(2)
|
then divide the result by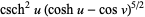 
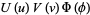to obtain
 |
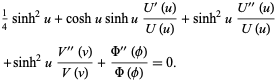(3)
|
The function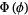 
then separates with
 |
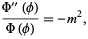(4)
|
giving solution
 |
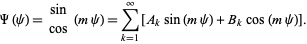(5)
|
Plugging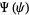 
back in and dividing by 
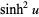gives
 |
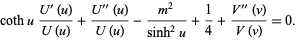(6)
|
The function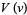 
then separates with
 |
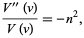(7)
|
giving solution
 |
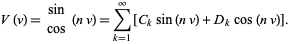(8)
|
Plugging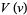 
back in and multiplying by 
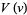gives
 |
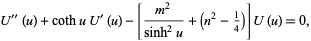(9)
|
which can also be written
 |
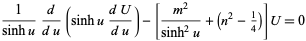(10)
|
(Arfken 1970, pp. 114-115). Laplace's equation is partially separable, although the Helmholtz differential equation is not.
Solutions to the differential equation for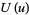 
are known as toroidal functions.
REFERENCES:
Arfken, G. "Toroidal Coordinates 
." §2.13 in Mathematical Methods for Physicists, 2nd ed. Orlando, FL: Academic Press, pp. 112-115, 1970.
Byerly, W. E. An Elementary Treatise on Fourier's Series, and Spherical, Cylindrical, and Ellipsoidal Harmonics, with Applications to Problems in Mathematical Physics. New York: Dover, pp. 264-266, 1959.
Morse, P. M. and Feshbach, H. Methods of Theoretical Physics, Part I. New York: McGraw-Hill, p. 666, 1953.
الاكثر قراءة في المعادلات التفاضلية الجزئية
اخر الاخبار
اخبار العتبة العباسية المقدسة
