


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 5-7-2021
Date: 24-5-2021
Date: 27-6-2021
|
Let P1, P2, P3, P4, P5 and P6 be the vertices of a regular hexagon in the plane, listed in cyclic order, and let K be simplicial complex consisting of the triangles P1P2P3, P3P4P5 and P5P6P1, together with all the edges and vertices of these triangles. Then

It follows that c1 is a 1-cycle of K if and only if
m2 = m3, m4 = m5, m6 = m1
and
m1 + m7 = m3 + m8 = m5 + m9.
Moreover c1 is a 1-boundary of K if and only if
m2 = m3 = −m8, m4 = m5 = −m9, m6 = m1 = −m7.
We see from this that not every 1-cycle of K is a 1-boundary of K. Indeed
Z1(K) = {n1∂2τ1 + n2∂2τ2 + n3∂2τ3 + nz : n1, n2, n3, n ∈ Z},
where z = ρ7 + ρ8 + ρ9. Let θ:Z1(K) → Z be the homomorphism defined such that
θ (n1∂2τ1 + n2∂2τ2 + n3∂2τ3 + nz) = n
for all n1, n2, n3, n ∈ Z. Now
n1∂2τ1 + n2∂2τ2 + n3∂2τ3 + nz ∈ B1(K) if and only if n = 0.
It follows that B1(K) = ker θ. Therefore the homomorphism θ induces an isomorphism from H1(K) to Z, where H1(K) = Z1(K)/B1(K). Indeed H1(K) = {n[z] : n ∈ Z}, where z = ρ7 + ρ8 + ρ9 and [z] denotes the homology class of the 1-cycle z.
It is a straightforward exercise to verify that
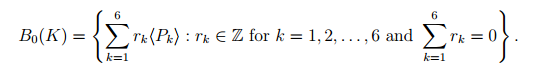
It follows from this that H0(K) ≅ Z. Indeed this result is a consquence of the fact that the polyhedron |K| of the simplicial complex K is connected.



|
|
|
|
التوتر والسرطان.. علماء يحذرون من "صلة خطيرة"
|
|
|
|
|
|
|
مرآة السيارة: مدى دقة عكسها للصورة الصحيحة
|
|
|
|
|
|
|
مؤتمر ذاكرة الألم في العراق يشهد انعقاد الجلسة البحثية الافتتاحية
|
|
|