Theorem 1.6 π₁(S¹, b) ≅Z for any b ∈ S¹.

Proof We regard S₁ as the unit circle in R². Without loss of generality, we can take b = (1, 0). Now the map p: R → S¹ which sends t ∈ R to (cos 2πt,sin 2πt) is a covering map, and b = p(0). Moreover p(t₁) = p(t₂) if and only if t₁ − t₂ is an integer; in particular p(t) = b if and only if t is an integer.

Let α and β be loops in S¹ based at b, and let ˜α and β˜ be paths in R that satisfy p ◦ α˜ = α and p ◦ β˜ = β. Suppose that α and β represent the same element of π₁(S¹, b). Then there exists a homotopy F: [0, 1] × [0, 1] → S₁

such that F(t, 0) = α(t) and F(t, 1) = β(t) for all t ∈ [0, 1], and F(0, τ ) = F(1, τ ) = b for all τ ∈ [0, 1]. It follows from the Monodromy Theorem  (Theorem 1.5) that this homotopy lifts to a continuous map G: [0, 1]×[0, 1] → R satisfying p ◦ G = F. Moreover G(0, τ ) and G(1, τ ) are integers for all τ ∈ [0, 1], since p(G(0, τ )) = b = p(G(1, τ )). Also G(t, 0)−α˜(t) and   G(t, 1)− β˜(t) are integers for all t ∈ [0, 1], since p(G(t, 0)) = α(t) = p(α˜ (t)) and p(G(t, 1)) = β(t) = p(β˜(t)). Now any continuous integer-valued function on [0, 1] is constant, by the Intermediate Value Theorem. In particular the functions sending τ ∈ [0, 1] to G(0, τ ) and G(1, τ ) are constant, as are the functions sending t ∈ [0, 1] to G(t, 0) − α˜(t) and G(t, 1) − β˜(t). Thus

G(0, 0) = G(0, 1),                     G(1, 0) = G(1, 1),  

G(1, 0) − α˜(1) = G(0, 0) − α˜(0),                 G(1, 1) − β˜(1) = G(0, 1) − β˜(0).

On combining these results, we see that

α˜(1) − α˜(0) = G(1, 0) − G(0, 0) = G(1, 1) − G(0, 1) = β˜(1) − β˜(0)

We conclude from this that there exists a well-defined function λ: π₁(S¹, b) → Z characterized by the property that λ([α]) = α˜ (1)−α˜(0) for all loops α based at b, where                   α˜: [0, 1] → R is any path in R satisfying p ◦ α˜ = α.

Next we show that λ is a homomorphism. Let α and β be any loops based at b, and let α˜ and β˜ be lifts of α and β. The element [α][β] of π₁(S¹, b) is represented by the product path α.β, where

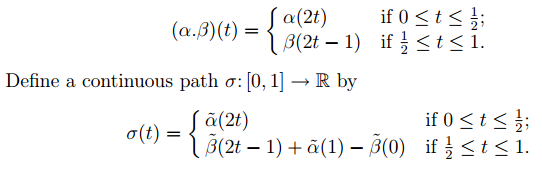
(Note that σ(t) is well-defined when t =1/2.) Then p ◦ σ = α.β and thus

 λ([α][β]) = λ([α.β]) = σ(1) − σ(0) = α˜ (1) − α˜(0) + β˜(1) − β˜(0)

                 = λ([α]) + λ([β]).

Thus λ: π₁(S¹, b) → Z is a homomorphism.

Now suppose that λ([α]) = λ([β]). Let F: [0, 1] × [0, 1] → S¹ be the homotopy between α and β defined by

              F(t, τ ) = p( (1 − τ ) α˜ (t) + τβ˜(t) ),

where α˜ and β˜ are the lifts of α and β respectively starting at 0. Now β˜(1) = λ([β]) = λ([α]) = α˜ (1), and β˜(0) = α˜ (0) = 0. Therefore F(0, τ ) = b = p(α˜ (1)) = F(1, τ ) for all              τ ∈ [0, 1]. Thus α ≃β rel {0, 1}, and therefore  [α] = [β]. This shows that λ: π₁(S¹, b) → Z is injective.

The homomorphism λ is surjective, since n = λ([γ_n]) for all n ∈ Z, where the loop γ_n: [0, 1] → S¹ is given by γ_n(t) = p(n_t) = (cos 2πnt,sin 2πnt) for all t ∈ [0, 1]. We conclude that                   λ: π₁(S¹ , b) → Z is an isomorphism.

We now show that every continuous map from the closed disk D to itself has at least one fixed point. This is the two-dimensional version of the Brouwer Fixed Point Theorem.

Theorem 1.7 Let f: D → D be a continuous map which maps the closed disk D into itself. Then f(x₀) = x₀ for some x₀ ∈ D Proof Let ∂D denote the boundary circle of D. The inclusion map i: ∂D → D induces a corresponding homomorphism  i_#: π₁(∂D, b) → π₁(D, b)of fun damental groups for any b ∈∂D.

Suppose that it were the case that the map f has no fixed point in D.

Then one could define a continuous map r: D → ∂D as follows: for each x ∈ D, let r(x) be the point on the boundary ∂D of D obtained by continuing the line segment joining f(x) to x beyond x until it intersects ∂D at the point r(x). Note that r|∂D is the identity map of ∂D.