Boundary Conditions

Since the function |Ψ(x. t)|² represents the probability density function, then for a single particle. we must have that

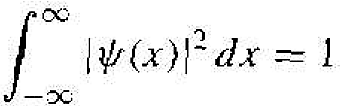(1)

The probability of finding the particle somewhere is certain. Equation (1) allows us to normalize the wave function and is one boundary condition that is used to determine some wave function coefficients.

The remaining boundary conditions imposed on the wave function and its derivative are postulates. However. we may state the boundary conditions and present arguments that justify why they must be imposed. The wave function and its first derivative must have the following properties if the total energy E and the potential V(x) are finite everywhere.

Condition 1. ѱ (x) must be finite, single-valued, and continuous.

Condition 2. ∂ѱ (x)/∂x must be finite, single-valued, and continuous.

Since |ѱ(x)|² is a probability density, then ѱ(x) must be finite and single-valued. If the probability density were to become infinite at some point in space, then the probability of finding the particle at this position would be certain and the uncertainty principle would be violated. If the total energy E and the potential V(x) are finite everywhere, the second derivative must be finite, which implies that the first derivative must be continuous. The first derivative is related to the particle momentum, which must be finite and single-valued. Finally, a finite first derivative implies that the function itself must be continuous. In some of the specific examples that we will consider, the potential function will become infinite in particular regions of space. For these cases. the first derivative will not necessarily be continuous, but the remaining boundary conditions will still hold.