
تاريخ الفيزياء

علماء الفيزياء


الفيزياء الكلاسيكية

الميكانيك

الديناميكا الحرارية


الكهربائية والمغناطيسية

الكهربائية

المغناطيسية

الكهرومغناطيسية


علم البصريات

تاريخ علم البصريات

الضوء

مواضيع عامة في علم البصريات

الصوت


الفيزياء الحديثة


النظرية النسبية

النظرية النسبية الخاصة

النظرية النسبية العامة

مواضيع عامة في النظرية النسبية

ميكانيكا الكم

الفيزياء الذرية

الفيزياء الجزيئية


الفيزياء النووية

مواضيع عامة في الفيزياء النووية

النشاط الاشعاعي


فيزياء الحالة الصلبة

الموصلات

أشباه الموصلات

العوازل

مواضيع عامة في الفيزياء الصلبة

فيزياء الجوامد


الليزر

أنواع الليزر

بعض تطبيقات الليزر

مواضيع عامة في الليزر


علم الفلك

تاريخ وعلماء علم الفلك

الثقوب السوداء


المجموعة الشمسية

الشمس

كوكب عطارد

كوكب الزهرة

كوكب الأرض

كوكب المريخ

كوكب المشتري

كوكب زحل

كوكب أورانوس

كوكب نبتون

كوكب بلوتو

القمر

كواكب ومواضيع اخرى

مواضيع عامة في علم الفلك

النجوم

البلازما

الألكترونيات

خواص المادة


الطاقة البديلة

الطاقة الشمسية

مواضيع عامة في الطاقة البديلة

المد والجزر

فيزياء الجسيمات


الفيزياء والعلوم الأخرى

الفيزياء الكيميائية

الفيزياء الرياضية

الفيزياء الحيوية

الفيزياء العامة


مواضيع عامة في الفيزياء

تجارب فيزيائية

مصطلحات وتعاريف فيزيائية

وحدات القياس الفيزيائية

طرائف الفيزياء

مواضيع اخرى
The Wave Equation
المؤلف:
Donald A. Neamen
المصدر:
Semiconductor Physics and Devices
الجزء والصفحة:
p 30
13-5-2017
2339
The Wave Equation
The one-dimensional, nonrelativistic Schrodinger's wave equation is given by
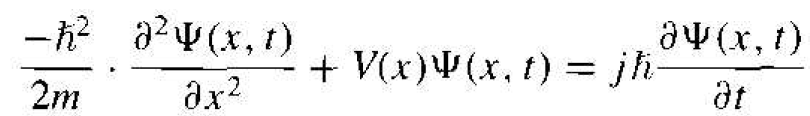 (1)
(1)
where Ψ (x, t) is the wave function, V(x) is the potential function assumed to be independent of
time, m is the mass of the particle, and j is the imaginary constant 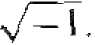 . There are theoretical arguments that justify the form of Schrodinger's wave equation. hut the equation is a basic postulate of quantum mechanics. The wave function Ψ (x, t) will be used to describe the behavior of the system and, mathematically, Ψ (x, t) can be a complex quantity.
. There are theoretical arguments that justify the form of Schrodinger's wave equation. hut the equation is a basic postulate of quantum mechanics. The wave function Ψ (x, t) will be used to describe the behavior of the system and, mathematically, Ψ (x, t) can be a complex quantity.
We may determine the time-dependent portion of the wave function and the position-dependent, or time-independent, portion of the wave function by using the technique of separation of variables. Assume that the wave function can he written in the form
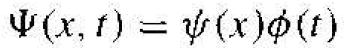 (2)
(2)
where ѱ(x) is a function of the position x only and ϕ(t) is a function of time t only. Substituting this form of the solution into Schrodinger's wave equation, we obtain
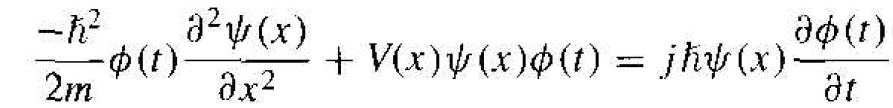 (3)
(3)
If we divide by the total wave function. Equation (3) becomes
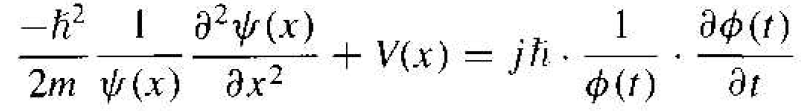 (4)
(4)
Since the left side of Equation (4) is a function of position x only and the right side of the equation is a function of time t only, each side of this equation must he equal to a constant. We will denote this separation of variables constant by η.
The time-dependent portion of Equation (4) is then written as
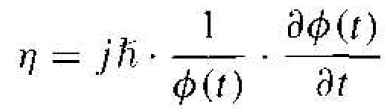 (5)
(5)
where again the parameter η is called a separation constant. The solution of Equation (5) can be written in the form
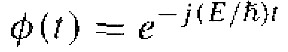 (6)
(6)
The form of this solution is the classical exponential form of a sinusoidal wave where η/h is the radian frequency ω. We have that E = hv or E = hω/2π. Then ω = q/h = E/h so that the separation constant is equal to the total energy E of the particle.
The time-independent portion of Schrodinger's wave equation can now he written from Equation (4) as
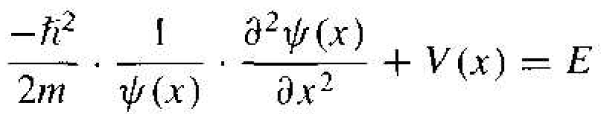 (7)
(7)
where the separation constant is the total energy E of the particle. Equation (7) may he written as
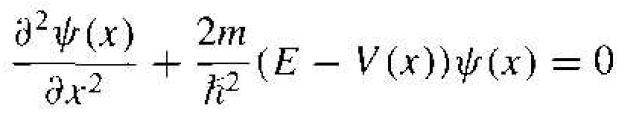 (8)
(8)
where again m is the mass of the particle, V(x) is the potential experienced by the particle, and E is the total energy of the particle. This time-independent Schrodinger's wave equation can also be justified on the basis of the classical wave equation as shown in Appendix E. The pseudo-derivation in the appendix is a simple approach but shows the plausibility of the time-independent Schrodinger's equation.
 الاكثر قراءة في ميكانيكا الكم
الاكثر قراءة في ميكانيكا الكم
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة

الآخبار الصحية















 قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة
قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة "المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة
"المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة (نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)
(نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)


















