
تاريخ الفيزياء

علماء الفيزياء


الفيزياء الكلاسيكية

الميكانيك

الديناميكا الحرارية


الكهربائية والمغناطيسية

الكهربائية

المغناطيسية

الكهرومغناطيسية


علم البصريات

تاريخ علم البصريات

الضوء

مواضيع عامة في علم البصريات

الصوت


الفيزياء الحديثة


النظرية النسبية

النظرية النسبية الخاصة

النظرية النسبية العامة

مواضيع عامة في النظرية النسبية

ميكانيكا الكم

الفيزياء الذرية

الفيزياء الجزيئية


الفيزياء النووية

مواضيع عامة في الفيزياء النووية

النشاط الاشعاعي


فيزياء الحالة الصلبة

الموصلات

أشباه الموصلات

العوازل

مواضيع عامة في الفيزياء الصلبة

فيزياء الجوامد


الليزر

أنواع الليزر

بعض تطبيقات الليزر

مواضيع عامة في الليزر


علم الفلك

تاريخ وعلماء علم الفلك

الثقوب السوداء


المجموعة الشمسية

الشمس

كوكب عطارد

كوكب الزهرة

كوكب الأرض

كوكب المريخ

كوكب المشتري

كوكب زحل

كوكب أورانوس

كوكب نبتون

كوكب بلوتو

القمر

كواكب ومواضيع اخرى

مواضيع عامة في علم الفلك

النجوم

البلازما

الألكترونيات

خواص المادة


الطاقة البديلة

الطاقة الشمسية

مواضيع عامة في الطاقة البديلة

المد والجزر

فيزياء الجسيمات


الفيزياء والعلوم الأخرى

الفيزياء الكيميائية

الفيزياء الرياضية

الفيزياء الحيوية

الفيزياء العامة


مواضيع عامة في الفيزياء

تجارب فيزيائية

مصطلحات وتعاريف فيزيائية

وحدات القياس الفيزيائية

طرائف الفيزياء

مواضيع اخرى
The Step Potential Function
المؤلف:
Donald A. Neamen
المصدر:
Semiconductor Physics and Devices
الجزء والصفحة:
p 38
9-5-2017
4278
The Step Potential Function
Consider now a step potential function as shown in Figure 1.1. In the previous section. we considered a particle being confined between two potential harriers. In this example, we will assume that a flux of particles is incident on the potential barrier. We will assume that the particles are traveling in the +x direction and that they originated at x = -∞. A particularly interesting result is obtained for the case when the total energy of the particle is less than the barrier height, or E < V0.
We again need to consider the time-independent wave equation in each of the two regions. This general equation was give as ∂2ѱ(x)/∂x2 + 2m/h2(E - V(x))ѱ(x) = 0. The wave equation in region I, in which V = 0, is
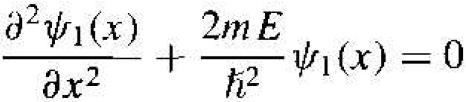 (1)
(1)
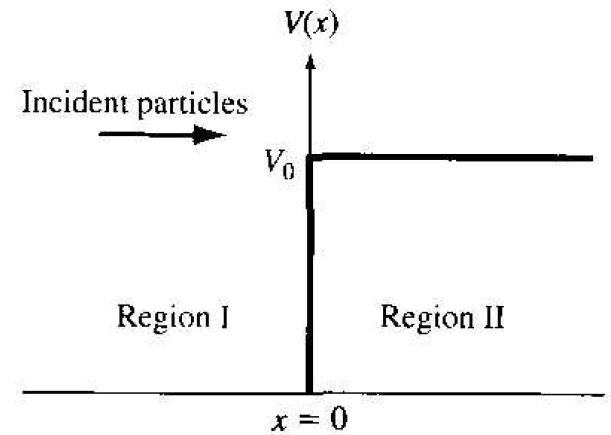
Figure 1.1 The step potential function.
The general solution to this equation can be written in the form
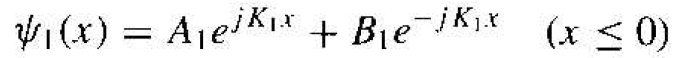 (2)
(2)
where the constant K1 is
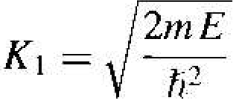 (3)
(3)
The first term in Equation (2) is a traveling wave in the +x direction that represents the incident wave, and the second term is a traveling wave in the -x direction that represents a reflected wave. As in the case of a free particle, the incident and reflected particles are represented by traveling waves.
For the incident wave, A1 . A*1 is the probability density function of the incident panicles. If we multiply this probability density function by the incident velocity, then vi . A1 . A*1 is the flux of incident particles in units of #/cm2-s. Likewise, the quantity vr . B1 . B*1 is the flux of the reflected particles, where vr is the velocity of the reflected wave. (The parameters vi and vr in these terms are actually the magnitudes of the velocity only.)
In region II, the potential is V = V0. If we assume that E < V0, then the differential equation describing the wave function in region II can be written as
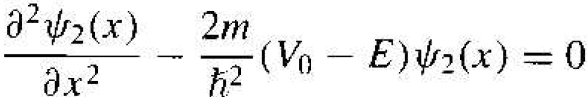 (4)
(4)
The general solution may then be written in the form
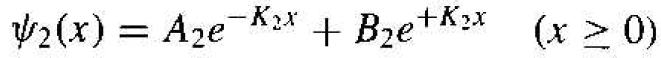 (5)
(5)
where
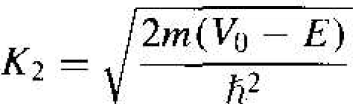 (6)
(6)
One boundary condition is that the wave function ѱ2(x) must remain finite, which means that the coefficient B2 = 0. The wave function is now given by
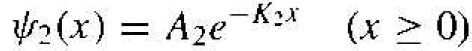 (7)
(7)
The wave function at x = 0 must be continuous so that
 (8)
(8)
Then from Equations (2), (7) and (8), we obtain
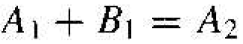 (9)
(9)
Since the potential function is everywhere finite, the first derivative of the wave function must also be continuous so that
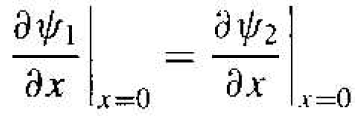 (10)
(10)
Using Equations (2), (7), and (10), we obtain
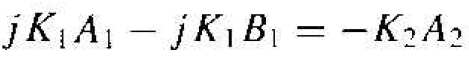 (11)
(11)
We can solve Equations (9) and (11) to determine the coefficients B1 and A2 in terms of the incident wave coefficient Al. The results are
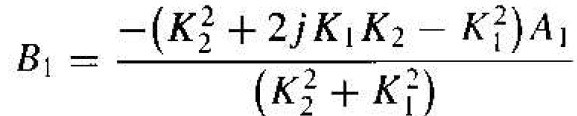 (12a)
(12a)
and
 (12b)
(12b)
The reflected probability density function is given by
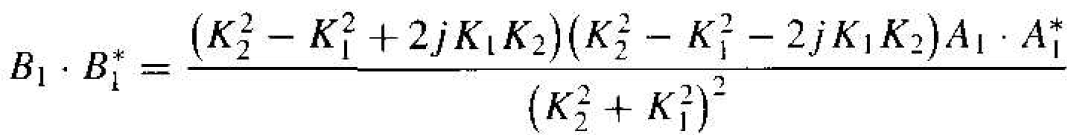 (13)
(13)
We can define a reflection coefficient, R, as the ratio of the reflected flux to the incident flux, which is written as
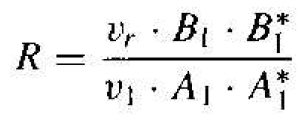 (14)
(14)
where vi and vr are the incident and reflected velocities. respectively. of the particles. In region I, V = 0 so that E = T, where T is the kinetic energy of the particle. The kinetic energy is given by
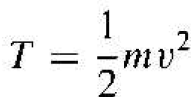 (15)
(15)
so that the constant Kl, from Equation (3), may be written as
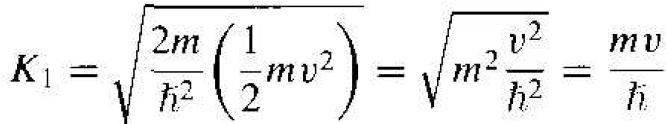 (16)
(16)
The incident velocity can then be written as
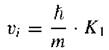 (17)
(17)
Since the reflected particle also exists in region I, the reflected velocity (magnitude) is given by
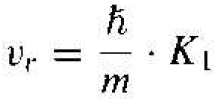 (18)
(18)
The incident and reflected velocities (magnitudes) are equal. The reflection coefficient is then
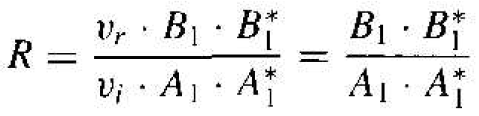 (19)
(19)
Substituting the expression from Equation (13) into Equation (19), we obtain
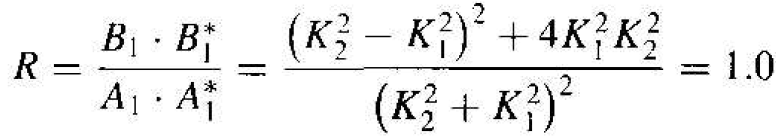 (20)
(20)
The result of R = 1 implies that all of the particles incident on the potential barrier for E < V0 are eventually reflected. Particles are not absorbed or transmitted through the potential barrier. This result is entirely consistent with classical physics and one might ask why we should consider this problem in terms of quantum mechanics. The interesting result is in terms of what happens in region II.
The wave solution in region II was given by Equation (7) as ѱ2(x) = A2e-K2x. The coefficient A2 from Equation (9) is A2 = A1 + B1 , which we derived from the boundary conditions. For the case of E < V0, the coefficient A2 is not zero. If A2 is not zero, then the probability density function ѱ2(x) . ѱ*2(x) of the particle being found in region II is not equal to zero. This result implies that there is a finite probability that the incident particle will penetrate the potential barrier and exist in region II. The probability of a particle penetrating the potential burrier is another difference between classical and quantum mechanics: The quantum mechanical penetration is classically not allowed. Although there is a finite probability that the particle may penetrate the barrier, since the reflection coefficient in region I is unity, the particle in region II must eventually turn around and move back into region I.
 الاكثر قراءة في ميكانيكا الكم
الاكثر قراءة في ميكانيكا الكم
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة

الآخبار الصحية















 قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة
قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة "المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة
"المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة (نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)
(نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)


















