


 الفيزياء الكلاسيكية
الفيزياء الكلاسيكية
 الكهربائية والمغناطيسية
الكهربائية والمغناطيسية
 علم البصريات
علم البصريات
 الفيزياء الحديثة
الفيزياء الحديثة
 النظرية النسبية
النظرية النسبية
 الفيزياء النووية
الفيزياء النووية
 فيزياء الحالة الصلبة
فيزياء الحالة الصلبة
 الليزر
الليزر
 علم الفلك
علم الفلك
 المجموعة الشمسية
المجموعة الشمسية
 الطاقة البديلة
الطاقة البديلة
 الفيزياء والعلوم الأخرى
الفيزياء والعلوم الأخرى
 مواضيع عامة في الفيزياء
مواضيع عامة في الفيزياء|
أقرأ أيضاً
التاريخ: 5-6-2017
التاريخ: 3-6-2017
التاريخ: 7-6-2017
التاريخ: 6-6-2017
|
انفصال الشحنات وشبه التعادل الكهربائي
البلازما هي مزيج من الجسيمات المشحونة هي الالكترونات المشحونة سلبا والايونات الايجابية الشحنة وفيها تتعادل تقريبا مجموع الشحنات السالبة للإلكترونات مع مجموعة الشحنات الموجبة للأيونات يدعى مثل هذا المزيج بالمزيج شبه المتعادل كهربائيا لانه متعادل تقريبا وسوف نرى ماذا تعني كلمة تقريبا في حالتنا هذه؟
سيؤدي كل فصل للشحنات الى ظهور حقول كهربائية مع العلم انه في البلازما الكثيفة ومهما كانت كثافتها تبدو هذه الحقول كبيرة الى حد غير قابل للقياس بناء على قوانين الكهرباء الساكنة اذا وجدت شحنة فراغية كثافتها q على بعد X من موضع توازنها فأنها تحدث حقلا كهربائيا qxπ E=4 في جملة الوحدات السغثية الكهربائية CGSE.
اذ تم قياس الحقل في الوحدات العملية VCM فانه يعبر عن ذلك بالعلاقة السابقة مضروبة بالعدد 300. بفرض ان في 1CM³توجد nΔ من الالكترونات الاضافية زيادة عما هو موجود لتأمين التعادل مع شحنة الايونات عندئذ تصبح كثافة الشحنة الفراغية:
Δn q = e
حيث e .شحنة الالكترونات في وحدات CGSE وتساوي 4.8×10-10 .
من هنا يكون الحقل الكهربائي الناتج عن انفصال الشحنات مساويا الى
ΔnxE=1.8×10-6
كمثال نأخذ بلازما ذات كثافة قريبة من كثافة الهواء الجوي عند سطح الارض أي :
5x1019 atom/cm او . 2.5×1019molecule/cm3 لنتصور ان هذا الهواء تحول الى بلازما أي ان كل ذرة فقدت الكترونا واحد هذا النوع هو اكثر انتشار من انواع البلازما وهي البلازما الحاوية على ايونات احادية الشحنة فقط . عندئذ يصبح تركيز الالكترونات مساويا:
n= 5.1019 electron/cm3
بفرض ان تركيز الالكترونات تغير بمقدار 1% على مسافة 1cm , عندئذ يكون:
= 5×1017e/cm3 nΔ
ونتيجة لهذا الانفصال في الشحنات يتولد حقل كهربائي شدته:
E= 9×1011 V/CM
من هذا المثال يتضح ان الانفصال الشحنات في البلازما الكثيفة مهمل لحد لا يمكن تصوره(1) لكي لا يتجاوز الحقل الكهربائي المتولد في مثالنا السابق حدا معقولا، وليكن 900V/CM فان المدى الذي يصل اليه انفصال الشحنات يجب الا يزيد على نسبة مئوية تقدر بجزء من المليار(!!!) ومن هنا تبرز صفة شبه التعادل للبلازما. ان تركيز الجسيمات الموجبة والسالبة يحقق شرط شبه التعادل بدقة عالية. لكن مهما كانت قيم الخروج عن شبه التعادل مهملة فان الحقول الكهربائية الناتجة عن ذلك تكون كبيرة وكبيرة جدا. في المثال المذكور أخذت بلازما كثيفة جدا. لكن غالبا ما يكون عملنا على البلازما المتخلخلة حيث يؤدي انفصال الشحنات الى حقول كهربائية اصغر بكثير في الكثير من التجارب المخبرية يمكن اعتبار البلازما النموذجية هي التي تكون ذات كثافة 1012 e/cm والتي تعطي انفصال الشحنات فيها بقدر 1% لمسافة 1cm حقلا كهربائيا تساوي شدته 1.8×104V/CM.
نرى ان حتى في البلازما المتخلخلة يبقى شرط التعادل محفوظا الى حد كاف على مسافة 1CMلكن اذا اخذنا شرط التعادل على مسافات مجهرية (ميكروسكوبية) فان انفصال الشحنات سيصبح ملموسا وهذا ينطبق ايضا على الفترات الزمنية القصيرة. وهكذا فان شرط شبه التعادل يعني التعادل الكهربائي وسطيا . على مسافات كبيرة وخلال فترات زمنية كافية.
يلعب البعد الفراغي للشحنات المنفصلة دورا هاما للغاية في فيزياء البلازما هذا البعد عبارة عن الطول الذي دونه يصبح انفصال الشحنات ملموسا راينا كيف انه كلما ازداد مدى انفصال الشحنات اشتد الحقل الكهربائي الناتج عن ذلك ومن اجل توليد حقل كهربائي تلزم طاقة فاذا انزاحت الالكترونات لمسافة X صغيرة اصبح الحقل الكهربائي 4πqx وسيحصل كل الكترون على طاقة قدرهاe/2 24πqx عند غياب التأثيرات الخارجية تنتج هذه الطاقة عن الطاقة الحرارية وحدها ان انفصال الشحنات يمكن ان يحصل تلقائيا على بعد x اذا لم تتجاوز الطاقة الكهربائية الساكنة الطاقة الحرارية أي:
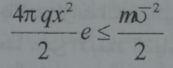
حيث v سرعة الحركة الحرارية الالكترونات .
ومن هنا يكون :
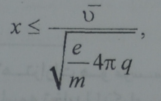
الطرف الايمن لهذه المتراجحة يشكل البعد الفراغي لانفصال الشحنات من اجل الانفصال الكامل للشحنات يلزم ان تنزاح الالكترونات كلها ويكون عندئذ:
n, q=en=n Δ
فيكون البعد الفراغي لانفصال الشحنات والذي سنرمز له ب h (دون ان نخلط بينه وبين ثابت بلانك!) محدد بالعبارة:
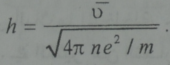
يعد الزمن الذي تستغرقه الجسيمة المتحركة بسرعة حرارية وسطية لكي تقطع هذه المسافة المقياس الزمني لانفصال الشحنات ويعطي بالعلاقة Ʋ 1=h/ .
يمكن لشرط شبه التعادل ان يختل خلال ازمنة اقل من المقياس الزمني مما يؤدي الى اهتزازات سريعة في كثافة الشحنة.
هذه الاهتزازات تلازم البلازما الى حد بعيد ولذلك تسمى الاهتزازات البلازمية(على الرغم من انه يمكن ان يكون في البلازما كثير من الاهتزازات الاخرى المتنوعة) ويدعى تواتر هذه الاهتزازات بالتواتر البلازمي وبما انه يحصل خلل في شبه التعادل خلال اهتزازه بلازمية واحدة فان تواتر الاهتزازات البلازمية يجب ان يكون من مرتبه مقلوب الزمن القياس 1/t حيث الزمن القياسي لانفصال الشحنات في البلازما وكما سنرى لاحقا في نموذج السائلين تبين الحسابات بان مقلوب الزمن القياسي يساوي بدقة التواتر الدائري لاهتزازت البلازما أي:
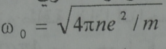
اما التواتر الخطي الاعتيادي فيساوي:
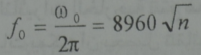
حيث f0 عدد الاهتزازات في الثانية. n عدد الالكترونات في 1cm3 وتسمى الاهتزازت البلازمية بالاهتزازات الكهربائية الساكنة ايضا(2).
والى هنا نكون قد اطلعنا على الابعاد القياسية لانفصال الشحنات من اجل الالكترونات اذ ان الالكترونات كجسيمات اكثر حركية غالبا ما تكون مسؤولة عن الانفصال الشحنات ولكن ويمكن ان ندرس انفصال الشحنات الناتجة عن ازاحة الايونات بطريقة متشابهة لا تقل عنها دقة.
يمكن ان تتكون البلازما من جسيمات مختلفة الانواع والتي نميزها بالدليل k سالبها وموجبها ونميز كل نوع من الجسيمات بكتلتهاMK وعدد شحناتها ZK بحيث ان شحنة كل جسيمة تساوي ZKE و e هي شحنة الالكترون.
وبما ان الالكترونات تكون في أي بلازما احد مركباتها دوما والتي من اجلها يكون M=m Z=1 وتكون الجسيمات المتبقية هي الايونات الموجبة التي سنميزها بالدليل i وبكتلة MI والشحنة ZI I يمكن كتابة شرط شبه التعادل بالشكل:
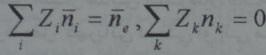
حيث تدل nعلى تركيز الجسيمات المعنية أي على عدد الجسيمات في وحدة الحجم، Ʃ يعني المجموع ويدل الخط فوق الرمز n على القيمة الوسطية سواء بالزمن او بالفراغ.
لكل نوع من الجسيمات تواتره البلازمي الخاص به ويعبر عن التواتر البلازمي الدائري ω0 من اجل الجسيمات ذات عدد شحنة Zوالكتلة M عموما بالعلاقة:
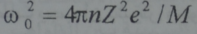
اما المقياس الزمني لانفصال الشحنات لهذا النوع من الجسيمات فيعطي 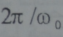 والمقياس الفراغي هو:
والمقياس الفراغي هو: 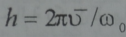 .
.
كلما ازدادت كثافة البلازما ازداد التواتر البلازمي وبالتالي كان المقياسان الزمني والفراغي لانفصال الشحنات اقل وتكون البلازما الكثيفة دوما متعادلة كهربائيا وتكون حركة الجسيمات فيها من نوع اخر بحيث لا تستطيع الايونات ترك الالكترونات وهذه الحركة تدعى بالحركة الجماعية . اما بالنسبة للبلازما المتخلخلة فان المقياس الفراغي لانفصال الشحنات يمكن ان يكون اكبر من الابعاد التي تشغلها البلازما نفسها . في مثل هذه الحالة تتحرك الجسيمات تلقائيا بشكل مستقل بعضها عن البعض الاخر .
ان شرط شبه التعادل لا يتحقق هنا وان تسمية مثل هذه الجملة بالبلازما يكون غير ذي معنى.
وهكذا يمكن ان نعطي التعريف التالي للبلازما : البلازما هي جملة جسيمات مشحونة مجموع شحناتها يساوي الصفر والتي يكون المقياس الفراغي لانفصال الشحنات فيها اصغر كثيرا من ابعاد الحيز الذي تشغله نفسها.
____________________________________
(1) تلزم طاقة هائلة لتوليد مثل هذا الحقل القوي عن مثل هذا الموضوع سيجري الحديث فيما بعد.
(2) ان اول من درس هذه الاهتزازات هو مؤسس فيزيائية البلازما العالم لانغمور والتي تسمى احيانا باسمه تخليدا لذكراه.



|
|
|
|
التوتر والسرطان.. علماء يحذرون من "صلة خطيرة"
|
|
|
|
|
|
|
مرآة السيارة: مدى دقة عكسها للصورة الصحيحة
|
|
|
|
|
|
|
مؤتمر ذاكرة الألم في العراق يشهد انعقاد الجلسة البحثية الافتتاحية
|
|
|