


 الفيزياء الكلاسيكية
الفيزياء الكلاسيكية
 الكهربائية والمغناطيسية
الكهربائية والمغناطيسية
 علم البصريات
علم البصريات
 الفيزياء الحديثة
الفيزياء الحديثة
 النظرية النسبية
النظرية النسبية
 الفيزياء النووية
الفيزياء النووية
 فيزياء الحالة الصلبة
فيزياء الحالة الصلبة
 الليزر
الليزر
 علم الفلك
علم الفلك
 المجموعة الشمسية
المجموعة الشمسية
 الطاقة البديلة
الطاقة البديلة
 الفيزياء والعلوم الأخرى
الفيزياء والعلوم الأخرى
 مواضيع عامة في الفيزياء
مواضيع عامة في الفيزياء|
Read More
Date: 6-2-2017
Date: 12-7-2020
Date: 19-8-2020
|
The Galactic rotation curve
The overall rotation of the Milky Way can only be derived if the movement of objects that closely trace the rotation of the disk can be analyzed throughout the Milky Way. Thus, an extinction-free tracer that is part of the disk (not the halo) is needed. Radioastronomical observations of neutral atomic or molecular gas clouds provide us with such a tracer.
If we assume that a gas cloud moves on a circular orbit around the Galactic Center, the ‘Galactic Structure Equation’ can be derived:
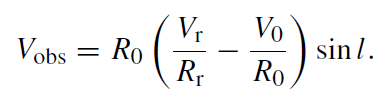
Here, Vobs is the observed radial velocity, Vr is the velocity at distance r , V0 is the orbital velocity of the Sun, Rr denotes the distance from the Galactic Center of a cloud at distance r from the Sun, R0 is the distance of the Sun from the Galactic Center and l is the Galactic longitude of the cloud at r. We have V0 ≈ 220 km s−1 and R0 ≈ 8 kpc. The radial velocity of the gas cloud can be observed readily and with high precision from spectral lines, e.g. the 21 cm hyperfine structure transition of H I or the 2.6 mm J = 1 → 0 rotational transition of the CO molecule.
From the Galactic structure equation we expect Vobs = Vobs(l) to be a family of sine curves. If this relation is plotted in a ‘longitude–velocity diagram’ (e.g. Burton 1895, Hartmann and Burton 1997 for H I, based on the Leiden-Dwingeloo Survey of neutral hydrogen or Dame et al 2001 for molecular gas), the expected behavior is indeed seen to a good approximation, with the exception of the region close to the Galactic Center, where the assumption of circular orbits breaks down. The rotation curve of the Galaxy, i.e. Vrot = Vrot(R), can be derived by considering a special case of the Galactic structure equation, using the classical tangent point method. If a cloud is located at the tangent point of the line of

Figure 1.1. A recent Galactic rotation curve (from Olling and Merrifield 2000). In general, the rotation curve can be described as flat; the slight rise in the outer part is model dependent and changes with, e.g., the assumed distance of the Sun to the Galactic Center. A possible deconvolution into components is given: long dashes, dark matter halo; filled circles, stellar disk; short dashes, bulge; open circles, molecular gas; and crosses, neutral hydrogen.
sight to a (circular) orbit around the Galactic Center, its entire orbital velocity will appear radial. For all realistic mass distributions, this results in the observed ‘tangential’ velocity being the highest velocity seen in a given spectrum, a quantity that is easy to determine. Then, we have
Vobs,tang = V (Rtang) − V(R0) sin l.
The distance Rtang of the tangent point from the Galactic Center is easily calculated as Rtang = R0 sin l. Thus, the rotation curve can be constructed, at least for R < R0, i.e. within the Solar circle.
In detail, a more careful analysis of non-circular contributions and the used position of the gas clouds is, of course, necessary, since there is not necessarily a gas cloud at any tangent point and non-circular motions, e.g. streaming motions in spiral arms, certainly exist (e.g. Malhotra 1995). The method breaks down in a region within the influence of the bar, i.e. in the inner 2-3 kpc.
Clearly, outside the Solar circle, a tangent point no longer exists. Thus, only Vr/Rr can be determined from the radial velocities. Distances have to be derived in some other way and are often inaccurate. The difference in error bars between the rotation curve inside and outside the Solar circle is striking (e.g. Olling and Merrifield 2000). Still, all determinations of the rotation of the Milky Way disk agree in one basic fact: after a brief, solid-body-like rise out to r ∼ 2–3 kpc, the rotation curve of the Galaxy is flat out to r > 20 kpc, reaching a maximum value which is obviously close to the Solar rotation velocity, 220 km s−1. Dehnen and Binney (1998) argue that a really flat rotation can only be derived if the distance of the Sun to the Galactic Center is ≤ 7.5 kpc. Otherwise, the rotation curve rises slightly.
The measured rotation curve can be decomposed into contributions due to the various constituents of the Galaxy, most importantly the bulge, the stellar disk, a (neutral and molecular) gas layer and the (dark) halo. Often, a ‘maximum disk’, i.e. a solution assigning the maximum possible mass to the stellar disk, based on the M/L ratio, is assumed. Even in this case, the only feasible models require a dark halo that dominates the mass budget in the outer part of the Galaxy, roughly outside the Solar circle. A recent example of a possible Galactic rotation curve and its deconvolution is given in figure 1.1.
Flat or even slightly rising rotation curves are a universal phenomenon for disk galaxies. Often, they can be more easily determined, based on H I emission, for external galaxies than for the Milky Way. Consequently, a large number has been measured, often to radii well outside the optical disk, since the neutral hydrogen, in many cases, extends beyond the stellar disk (e.g. Bosma 1981, Sofue 1996, 1997). All disk rotation curves without exception seem to be flat out to the limits of observability. The only difference between various Hubble types, i.e. spiral galaxies with more or less pronounced bulges, seems to be that ‘earlier’ Hubble types, Sa and Sb galaxies with stronger bulges, tend to reach a somewhat higher plateau value than later Hubble types (Sc and Sd spirals, Rubin et al 1985).
This is the main argument for the universal need for dark matter on galactic scales, a need that seems compelling, as long as one does not want to resort to modifications to the law of gravity (MOND—Modified Newtonian Dynamics theories, Milgrom 1983 and many subsequent papers) which seem, however, ad hoc and unconvincing from a theoretical point of view. Dark matter is also needed, for other reasons, on the larger scale of clusters of galaxies.
A rotation curve is, of course, a global, azimuthally averaged, property of a galaxy. Some hints of the details exist, e.g. in the small ‘wiggles’ visible in many rotation curves, pointing to streaming motions due to the influence of spiral arms. However, such details dominate the visual appearance of spiral galaxies like the Milky Way.



|
|
|
|
دراسة يابانية لتقليل مخاطر أمراض المواليد منخفضي الوزن
|
|
|
|
|
|
|
اكتشاف أكبر مرجان في العالم قبالة سواحل جزر سليمان
|
|
|
|
|
|
|
اتحاد كليات الطب الملكية البريطانية يشيد بالمستوى العلمي لطلبة جامعة العميد وبيئتها التعليمية
|
|
|