


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 5-1-2017
Date: 23-2-2019
Date: 10-1-2017
|
To show that the set of propositions and the operations of conjunction, disjunction, and negation form a Boolean algebra, it is necessary first to define the concept of equality. Two propositional functions g and h, each functions of the n propositional variables p1, p2, ... , pn, are said to be equal if and only if they have the same truth value for every possible way of assigning truth values to each of the n variables. For example, if g and h are each functions of the two variables p and q, we can determine whether they are equal by checking the truth values of g and h separately for each of the four possibilities: p false and q true; p true and q false; p and q both true; and p and q both false. If the results are the same for each case, g and h are equal. If their truth values differ for any case, they are unequal.
This definition may sound strange at first, but it would be difficult to use any other definition. Certainly, a definition based on the words used to express the proposition would be impossible because there are many ways of wording a single statement in English alone, to say nothing of the possibilities if an arbitrary language is used. Similarly, there is no way in which the meaning conveyed by the proposition can be employed. Meaning is an intangible thing, impossible to treat in a precise way. The truth value, on the other hand, is specific, and by our assumption is always one of two things, truth or falsehood, for each proposition. As soon as the symbols 0 and 1 are introduced, we will see that this definition reflects the fact expressed in the corollary (Two functions are equal if and only if their respective disjunctive normal forms contain the same terms.)that a function is completely determined when its value is known for each possible assignment of 0 and 1 to the variables involved.
To complete our algebra, we will create two new propositions represented by 0 and 1, respectively. We define 0 to be a proposition that is always false, and 1 to be a proposition that is always true. The equation p = 0 is equivalent to the statement that p is false. Similarly, q = 1 is equivalent to saying that q is true.
The definition we have given for equality makes it possible to represent a function with a table of values exactly as was done in Section (Disjunctive normal form).
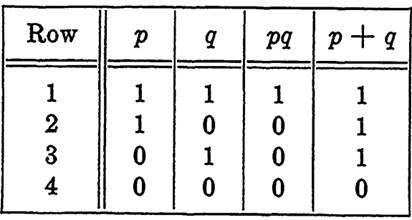
The only difference is that now we have a special meaning attached to the symbols which appear in the table. These symbols stand for propositions rather than for abstract elements of an arbitrary Boolean algebra. Such a table will be termed a truth table. An example of such a table is Table 1-1 for the functions pq and p + q. In reading this table, row 3, for instance, presents the information that pq is false and p + q is true if p is false and q is true.
TABLE 1-1
TRUTH TABLE FOR pq AND p + q
The construction of a truth table for a complicated propositional function can best be carried out in steps, using at each step the basic truth table for one of the operations (+), (.)or ('). For example, Table 1-2 shows the construction by steps of the truth table for the function (r' + pq)'. If it happens that the truth table for a function contains only 1's (in the function column), we call the corresponding proposition a tautology. Both p + p' and pq + pq' + p'q + p'q' are examples of tautologies for any propositions p and q.
TABLE 1-2
CONSTRUCTION OF THE TRUTH TABLE FOR (r' +pq)'
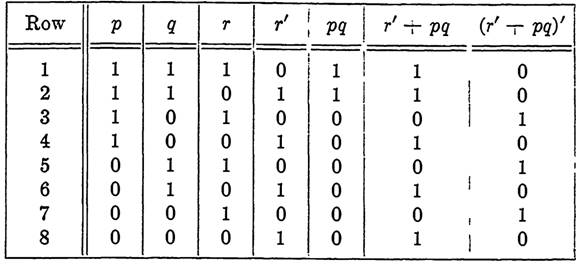
TABLE 1-3
TRUTH TABLE SHOWING p + qr = (p + q)(p + r)
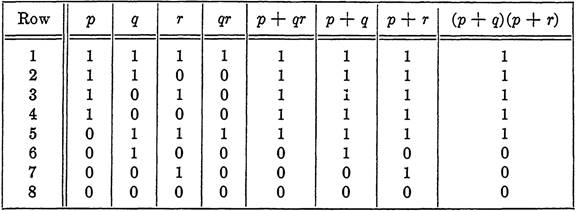
An illustration of the usefulness of truth tables occurs in the proof of the following theorem. From the definition of equality, it follows that two functions are equal if and only if their truth tables are identical. This fact is used in part (c) of the proof below.
THEOREM. The algebra of propositions is a Boolean algebra.
Proof. (a) That both (+) and(.) are commutative follows immediately from the definition and hence Postulate 1 (definition of Boolean algebra) holds.
(b) 0 is the identity element for the operation (+) since 0 + p has the same truth value as p and hence equals p. Similarly, (1) (q) has the same truth value as q and hence equals q, showing that 1 is the identity for the operation of conjunction.
(c) Each operation is distributive over the other. Table 1-3 establishes one distributive law, and the other is left to the reader.
(d) For each proposition, there is a second proposition p', the negation of p, which satisfies the relations pp' = 0 and p + p' = 1.
We have verified all four postulates for a Boolean algebra, and with this the proof of the theorem is complete. From now on we may use without special proof any result from Chapter of (Boolean algebra.) concerning Boolean algebra.
Not only can a truth table be constructed for a given propositional function, but if it happens that a truth table is known, then the corresponding propositional function may be found in exactly the same way as a general Boolean function was constructed in Sections (Disjunctive normal form) and (Conjunctive normal form). The following hypothetical problem illustrates this procedure.
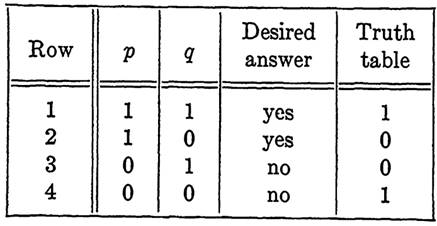
EXAMPLE. A logician was captured by a certain gang. The leader of the gang blindfolded the captive and placed him in a locked room containing two boxes. He gave the following instructions, "One box contains the key to this room, the other a poisonous snake. You are to reach into either box you choose, and if you find the key, you may use it to go free. To help you, you may ask my assistant a single question requiring a yes or no answer. However, he does not have to answer truthfully; he may lie if he chooses." After a moment of thought, the logician asked a question, reached into the box with the key, and left. What question did the logician ask so that he was certain to go free?
Solution. Let p be the proposition "the box on my left contains the key." Let q be the proposition "you are telling the truth." Suppose that we desire the answer "yes" if p is true, and "no" if p is false. The first three columns of Table 1-4 represent the possible truth values of p and q and the desired answers. The required proposition, then, must have column 4 as its truth table. To illustrate the reasoning used in forming the truth table, consider row 2. The values of p and q indicate that for this case, the key is in the left box and the man is lying. Consequently, to obtain an affirmative answer the function must have the value 0. The propositional function corresponding to this truth table is pq + p'q'. Hence the proper question is:
Is the proposition "the box on the left contains the key and you are telling the truth, or the box on the right contains the key and you are lying" a true proposition?
TABLE 1-4
We are assuming, of course, that the man who answers the question is intelligent enough to understand the question and that he either lies or tells the truth delib-
erately and does not answer in a random manner. A simpler wording is possible for the proposition, but the terminology has not yet been developed.



|
|
|
|
علامات بسيطة في جسدك قد تنذر بمرض "قاتل"
|
|
|
|
|
|
|
أول صور ثلاثية الأبعاد للغدة الزعترية البشرية
|
|
|
|
|
|
|
مكتبة أمّ البنين النسويّة تصدر العدد 212 من مجلّة رياض الزهراء (عليها السلام)
|
|
|