


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات | INTRODUCTION TO PROBABILITY IN FINITE SAMPLE SPACES-Event, sample space, probability |
|
|
|
Read More
Date: 29-12-2016
Date: 7-1-2017
Date: 12-1-2017
|
Statements such as "It is likely to rain tomorrow," "A bridge hand is not apt to contain four aces," and "If you have five children, it is probable that one or more of them are boys" are probability statements. One of the purposes for studying probability is the desire to make such statements quantitative. For example, the statement "If I flip a coin, the chances that it will turn up heads is one-half " is a quantitative statement of probability which is usually accepted as valid. The procedure followed in making such quantitative statements is to construct a mathematical model which appears to represent the case in question, then to use the methods of mathematical probability theory to analyze the model, and finally to apply the results to the practical case. Probability theory is concerned with mathematical models rather than with natural problems. That is, the theory of probability does not deal specifically with natural phenomena, but rather with abstract mathematical concepts. Its usefulness depends upon the ability of the investigator to construct a model which reasonably reflects the actual situation.
Suppose that we consider either a real or a conceptual experiment with a finite number N of possible outcomes. We will take a universal set to be the set of all outcomes and for any subset X, we define the probability of X to be the number P(X) = n(X)/N. We note that this definition implies immediately that P(1) = 1, P(0) = 0, and P(X') = 1 - P(X). In the language of probability, the universal set is referred to as the sample space, each subset is termed an event, and the unit sets are called sample points. P(X) is the ratio of the number of sample points in the event X to the number of sample points in the sample space, and is usually referred to as the probability of the occurrence of the event X.
In the above definition, the words experiment and outcome have been used to make the concepts intuitively meaningful. It should be pointed out, however, that these concepts are not part of the mathematical model. The model consists solely of a set of N arbitrary elements, the possible subsets of this set, and the numbers P(X) assigned to each subset X.
This model can be generalized in two ways, first by allowing a sample space with more than a finite number of distinct sample points, and also by assigning probabilities to sample points in an arbitrary manner, rather than requiring that each sample point have probability 1/N. Both of these generalizations are included in the usual courses in probability theory. The purpose of this chapter is to present an insight into the role which the algebra of sets plays in the theory, and for this purpose it will be sufficient to consider only the simplest case, as stated in our definition.
As the preceding paragraphs have suggested, the problem of choosing a suitable model is often the most difficult step in the formulation of accurate probability statements. As an illustration of a correct and an incorrect method of making the choice, consider the problem of determining the probability of the occurrence of a sum of 7 in rolling two dice.
FIRST MODEL. Suppose that we consider the possible "outcomes" to be the eleven possible sums 2, 3, ..., 12. That is, our sample space will have eleven points, and if X represents the event that a sum of 7 occurs, we have that P(X) = 1/11. Intuition tells us that this answer is not "correct," and in fact it does not represent the actual probability. It is not the mathematics that is at fault, but rather the choice of model. There are two ways in which the model could be changed to give a more reasonable answer. One is to assign probabilities in a different manner. Clearly 7 is more probable than 2 or 12. Since our definition of probability will not allow this change, we will consider the second possibility.
SECOND MODEL. Let the sample space consist of thirty-six points, each corresponding to a pair of numbers selected from the integers 1, 2, ... , 6. The firstnumber of the pair will represent the face appearing on the first die, the secondwill represent the face appearing on the second die. Thus (1, 1), (2, 5), and (5, 2) are each sample points. Again, let X be the event that 7 is the sum of the faces appearing on the two dice. X contains the six points (1, 6), (6, 1), (2, 5), (5, 2), (3, 4), and (4, 3). Hence P(X) = 6/36 = 1/6, which is a more reasonable answer than the first.
Both answers are mathematically correct, since each was correctly derived from the model. The second is, of course, more realistic. In more complicated applications, it may be difficult, or even impossible, to determine whether a given model fits the application closely enough, although the fit of a model may usually be tested in many ways. In the example above, for instance, one might roll two dice again and again, say six hundred times. If the result showed approximately one hundred occurrences of 7 we would tend to believe that the second model was well chosen.
In stating problems on probability concerning two events X and Y, the phrase "the probability of occurrence of X or Y" means the probability of the event X + Y, and "the probability of occurrence of X and Y" means the probability of the event XY.
EXAMPLE 1. A bag contains ten tags numbered 0, 1, 2, ..., 9. Let X be the event that a chance drawing results in 5 or 8, and Y be the event that a digit larger than 5 is drawn. Find the probabilities that (a) event X occurs, (b) event Y occurs, (c) event X or event Y occurs, and (d) event X and event Y occur.
Solution. The sample space contains 10 points, X contains 2 points, Y con tains 4 points, X + Y contains 5 points, and XY contains 1 point. The probabilities are therefore:

The following two theorems are direct consequences of theorems in (THE ALGEBRA OF SETS) and are useful in considering probabilities of combinations of events. We will say that two events are mutually exclusive in case the sets with which the events correspond are disjoint. Intuitively, mutually exclusive events are events which cannot occur simultaneously.
THEOREM 1. If A and B are mutually exclusive events, then P(AB) = 0 and P(A + B) = P(A) + P(B).
Proof. That P(AB) = 0 follows immediately from the definition of the phrase mutually disjoint. Since A and B represent disjoint sets, it follows from (The number of elements in a set) that n(A + B) = n(A) + n(B), and dividing both sides by N (the number of elements in the sample space), we have that P(A + B)=P(A) + P(B).
THEOREM 2. For arbitrary events A and B, P(A + B) = P(A) + P(B) - P(AB).
Proof. If the sample space in which events A and B occur contains N elements, then by definition, P(A + B) = n(A + B)/N. By Theorem 1 of (the number of elements in the sample space), n(A + B) = n(A) + n(B) - n(AB), and therefore
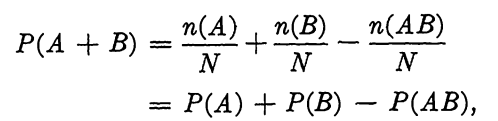



|
|
|
|
التوتر والسرطان.. علماء يحذرون من "صلة خطيرة"
|
|
|
|
|
|
|
مرآة السيارة: مدى دقة عكسها للصورة الصحيحة
|
|
|
|
|
|
|
دراسة تستعرض آلام السجناء السياسيين في حقبة البعث المجرم في العراق
|
|
|