The definition of a Boolean algebra which will be used here is the one given by Huntington in 1904. Many other sets of postulates could be chosen that would define the algebra equally well. This set has the property that no postulate can be derived from the remaining postulates.

DEFINITION. A class of elements B together with two binary operations  (+) and(.) (where a b will be written ab) is a Boolean algebra if and only if the following postulates hold:

P1. The operations (+) and(.) are commutative.

P2. There exist in B distinct identity elements 0 and 1 relative to the operations (+) and(.) respectively.

P3. Each operation is distributive over the other.

P4. For every a in B there exists an element a' in B such that

                                a+ a' = 1                    and                   aa' = 0.

There is no reason why the two operations in the definition must be written (+) and(.) Any two symbols would serve equally well. If a set with operations ∘ and *, or ⋃ and ⋂, satisfied the analogous postulates, it would be a Boolean algebra. (+) and (.) were chosen only to conform with the notation used in the other chapters.

THEOREM 1. Every statement or algebraic identity deducible from the postulates of a Boolean algebra remains valid if the operations (+)and (.)and the identity elements 0 and 1 are interchanged throughout.

(This theorem is known as the principle of duality.)

Proof. The proof of this theorem follows at once from the symmetry of the postulates with respect to the two operations and the two identities.  If one statement or algebraic expression is obtained from another by a single application of the principle of duality, the second is said to be the dual of the first. In this case, it is clear that the first is also the dual of the second. Each of the following theorems contains two dual statements,  with the exception of one in which the given proposition is its own dual.  From Theorem 1, it is necessary to prove only one of each pair of dual statements. However, to illustrate the nature of duality, both proofs are given in Theorem 2.

It should be noted that the steps in one proof are dual statements to those in the other, and the justification for each step is the same postulate or theorem in one case as in the other.

THEOREM 2. For every element a in a Boolean algebra B,

a + a = a                            and                     as = a.

Proof.     a = a + 0                                           by P₂

                   = a+aa'                                          by P₄

                   = (a + a) (a + a')                          by P₃

                    = (a + a) (1)                                by P₄

                       = a+ a,                                     by P₂

and similarly,

                        a = a(1)                                                   by P₂

                          = a(a + a')                                             by P₄

                         = as + ad                                                by P₃

                         = as+0                                                     by P₄

                          = aa.                                                        by P₂

THEOREM 3. For each element a in a Boolean algebra B,

                   a + 1 = 1             and                   a0 = 0.

Proof.           1 = a+ a'                                             by P₄

                         = a + a'(1)                                        by P₂

                        = (a + a') (a + 1)                              by P₃

                       = 1(a+1)                                            by P₄

                         =a+1.                                               by P₂

THEOREM 4. For each pair of elements a and b in a Boolean algebra B,

                    a + ab = a            and                         a(a + b) = a.

Proof.                   a= 1a                                       by P₂

                              =(1 + b)a                                 by Theorem 3

                             = 1a+ba                                   by P₃ and P₁

                             = a+ba                                       by P₂

                            = a+ab.                                        by P₁

THEOREM 5. In every Boolean algebra B, each of the binary operations  (+) and (.)is associative. That is, for every a, b, and c in B,

a + (b + c) = (a + b) + c                       and                            a(be) = (ab)c.

Proof. First we will show that   a + a(bc) = a + (ab)c,  as follows:

                       a + a(bc) = a                                   by Theorem 4

                                        = a(a + c)                       by Theorem 4

                                        = (a + ab) (a + c)         by Theorem 4

                                       = a + (ab)c.                    by P₃

Next we will show that a' + a(bc) = a' + (ab)c, as follows:

                   a' + a(bc) = (a' + a) (a' + bc)                            by P₃

                                    = 1(a' + bc)                                        by P₄

                                    = a'+bc                                                by P₂

                                   =(a' + b) (a' + c)                                 by P₃

                                  = [1(a' + b)](a' + c)                            by P₂

                                 =[(a' + a)(a'+ b)](a' + c)                     by P₄

                                = (a' + ab)(a' + c)                                  by P₃

                                 = a' + (ab)c.                                           by P₃   

Now if we multiply these two equations, we obtain

[a + a(bc)][a' + a(bc)] = [a + (ab)c][a' + (ab)c].                                 (1-1)

The left side of Eq. (1-1) may be reduced as follows:

               [a + a(bc)][a' + a(bc)] = [a(bc) + a][a(bc) + a'] by P₁

                                                        = a(bc) + aa'                    by P₃

                                                       = a(bc) + 0                       by P₄

                                                      = a(bc).                              by P₂

Similarly, the right side of (1-1) reduces as follows:

[a + (ab)c][a' + (ab)c] = [(ab)c + a][(ab)c + a']             by P₁

                                        = (ab)c + aa'                                 by P₃

                                       = (ab)c + 0                                     by P₄

                                       = (ab)c.                                           by P₂

Hence Eq. (1-1), when simplified, reads

                                                a(bc) = (ab)c,

and this statement is the associative law that we were to prove.

From now on, we shall write both a(bc) and (ab)c as abc, and similarly,  we shall write both (a + b) + c and a + (b + c) as a + b + c.

THEOREM 6. The element a' associated with the element a in a Boolean algebra is unique. (That is, only one element a' satisfies the conditions of P₄.)

Proof. Suppose that a + x = 1, ax = 0, and also that a + y = 1,  ay = 0. Then,

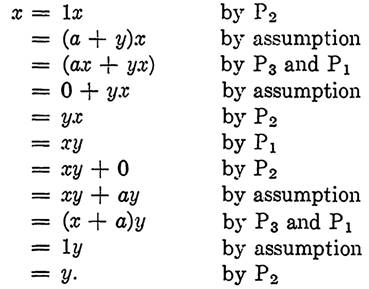
Thus any two elements associated with a as specified in P₄ are equal. In other words, a' is uniquely determined by a. We will refer to a' as the complement of a.

THEOREM 7. For every a in a Boolean algebra B, (a')' = a.

Proof. By P₄, a + a' = 1, and aa' = 0. But this is exactly the necessary condition that (a')' is equal to a. By Theorem 6, no other element has this property.

THEOREM S. In any Boolean algebra, 0' = 1 and 1' = 0.

Proof. By Theorem 3, 1 + 0 = 1, and (1)(0) = 0. Since Theorem 6 shows that for each a there is only one element a', these equations imply that 0' = 1, and 1' = 0.

THEOREM 9. For every a and bin a Boolean algebra B,

                              (ab)' = a' + b'                and                        (a + b)' = a'b'.

(ab) (a' + b') = aba' + abb'                                          by P₃

                       = 0b + a0 = 0 + 0 = 0.                     by P₁, P₂, P₄, Theorem 3

Further,

            Ab+a'+b'=a'+b'+ab                                                     by P₁

                             = (a'+b'+a)(a'+b'+b)                                    by P₃

                             = (1 + b') (1 + a')                                          by P₄ and P₁

                             = 1.                                                          by Theorem 3 and P₂

DEFINITION. The "order" relation a⊆b is defined by the statement:  For every a and bin a Boolean algebra B, a⊆b if and only if ab' = 0.

The following theorem contains the contents of four theorems in Section (Properties of set inclusion) which were derived there intuitively for sets. The proof here is based on the definition of the relation.

THEOREM 10. The following four properties of ⊆ are valid in every Boolean algebra for arbitrary elements x, y, and z:

(a) If x ⊆y and y ⊆ z, then x ⊆ z.

(b) If x ⊆⊆ y and x ⊆ z, then x ⊆ yz.

(c) If x⊆y,then x⊆y+zfor any z.

(d) x ⊆y if and only if y' ⊆ x'.

Proof. The reasons for the steps in the proofs have been omitted, but should be supplied by the reader.

(a) x c y is equivalent to xy' = 0 and y ⊆z is equivalent to yz' = 0.

Hence xz' = xz'(y + y') = xyz' + xy'z' = 0 + 0 = 0. But xz' = 0 is equivalent to x ⊆ z, which was to be shown.

(b) From x⊆y and x ⊆z we have xy' = 0 and xz' = 0. Hence xy' + xz' = 0 and x(y' + z') = 0. But by Theorem 9, y' + z' = (yz)' and thus x(yz)' = 0 or, equivalently, x ⊆ yz.

(c) From x ⊆ y we have xy' = 0 and hence x(y + z)' = x(y'z') = (xy')z' = 0. But x(y + z)' = 0 is equivalent to x⊆y + z and (c) is proven.