The question of how one should proceed to count the number of elements in a set is not, strictly speaking, a part of the algebra of sets. However, to demonstrate how the algebra of sets forms the basis of probability theory, we would like to investigate sample spaces of a more involved nature. To do so requires the use of the theory of permutations and combinations. This theory is essentially a counting technique, and will be discussed briefly for the benefit of readers who may not have the necessary background. Anyone familiar with this material may easily proceed to (Bernoulli trials, binomial distribution).

First, we shall define an ordered pair to be a special kind of set containing exactly two elements, with the additional property that we are able to distinguish one of the elements, called the first element, from the other, called the second element. We shall designate such pairs (x, y),  where x is the first element, and y is the second element. A fundamental principle of counting is the following:

If X and Y are any two sets with finitely many elements, the number of distinct ordered pairs (x, y) which can be formed with x ∈ X and y∈Y is n(X)n(Y).

The concept of ordered pairs is easily extended to the concept of ordered r-tuples, each of which is a set with exactly r elements, with the property that it is possible to determine uniquely a first, second, ... , rth element.  Such r-tuples are denoted by (X₁, x₂, ... , x_r). The fundamental principle extends to give the number of distinct r-tuples as the product of the numbers of elements which may be used for the respective positions.

DEFINITION. The number of permutations of n things taken r at a time,  0 ≤ r≤n, is defined to be the number of distinct r-tuples which can be formed from n elements, where it is assumed that no element can simultaneously appear twice in one r-tuple. This number is denoted by ,_nP_r.

THEOREM 1. The value of nPr is given by

                    _nP_r=n(n-1)(n-2)...(n-r-1)                    (1)

Proof. If we consider the definition of _nP_r, it is clear that the first element of the r-tuple is to be chosen from a set of n elements. Having chosen the first element, a set of n - 1 elements is left, from which the second may be chosen, etc. Hence the formula follows.

In the case r = n, Theorem 1 says that there are n(n - 1) (n - 2)  (2)(1) permutations of n things taken n at a time. This number appears so often that it is convenient to give it a special designation, n!. We will extend the definition of this symbol to the special case n = 0 by defining 0! to be the number 1. Using this new notation, Eq. (1) can also be written as

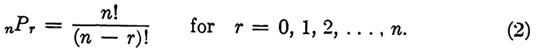
DEFINITION. The number of combinations of n things taken r at a time is defined to be the number of distinct subsets, each containing r elements, which are contained in a set with n elements. We denote this number by (ⁿ_r).

THEOREM 2. The value of (ⁿ_r) is given by

Proof. Clearly the distinction between the numbers ._nP_r and (ⁿ_r)is that (ⁿ_r)counts subsets only, whereas _nP_r counts each possible ordering within each subset. Hence the relation between the numbers is

This follows since, after a subset has been chosen, it may still be arranged in r! ways, by Theorem 1. If _nP_r in Eq. (4) is replaced by n!/(n - r) !  and both sides of the resulting equation are divided by r!, Eq. (3) is obtained.  In any particular problem, before these formulas are used, care must be taken to determine whether permutations or combinations are required.

Although no rules can be formulated to replace intelligent thinking, a guide to the correct choice is the decision as to whether "order" is important. In selecting a committee of three, where no significance is attached to being first, second, or third, it would be natural to use the idea of combinations. If, however, the first choice were to be chairman and the second choice secretary, it might be more natural to use the idea of permutations. That is, in this case we would consider the committee Jones,  president; Smith, secretary; and Brown as distinct from the committee Brown, president; Smith, secretary; and Jones.

EXAMPLE 1. How many distinct numbers of four digits, each having no repeated digits, can be formed from the digits 1, 2, 3, 4, 5, 6, 7?

Solution. The number is ₇P₄ = 7!/3! = 840.

EXAMPLE 2. How many different sums of money can be formed from one penny, one nickel, one dime, one quarter, and one half dollar?

Solution. Here order makes no difference, hence the answer is

EXAMPLE 3. Find the probability that a five-card poker hand will be a straight flush (five cards in sequence in a single suit, but not with ace high; the ace may be used as low card, however).

Solution. First, the choices of suit and of possible hands within a suit may be thought of as the choice of pairs of elements, the first from the set of suits,  the second from the set of allowable hands within suits, and hence the basic principle of counting may be applied. There are four possible suits, and a permissible hand may have as low card any of the nine cards A, 2, 3, ..., 9. The total number of five-card hands (corresponding to the number of elements in the sample space) is (⁵²₅ ). Hence the desired probability is (4) (9)/(⁵²₅), or approximately 0.000,014.