Global Positioning Satellites

The global positioning system (GPS) is a modern marvel, with a constellation of at least 24 satellites, each in a 12-hour orbit at an altitude of about 20,200 kilometers, whizzing around Earth at enormous speeds with respect to the ground beneath them. Each satellite knows its own position and sends out signals with this information. The GPS handheld receiver uses the signals from at least four different satellites to calculate its own position to within a few meters or better when a local reference signal is present. Yet within minutes the accuracy would reduce to many kilometers of error if one of Einstein’s discoveries were not an essential part of the calculations in the GPS system. What are we referring to?

Answer

The general theory of relativity (GTR) plays an important role! Corrections must be made for clock rates in a gravitational field in addition to the special theory of relativity (STR) corrections to the clocks for the movement of the satellite. Both relativistic effects foul up what should have been a pretty simple geometry calculation relating distance to time and velocity. The clocks in the satellites tick at a slightly faster rate than identical clocks on the ground because they are in a slightly weaker gravitational field, being farther from the center of Earth. They tick slower than the Earth-bound clocks because they are moving faster with respect to the stars.

We can estimate the sizes of these effects. From the STR, the time interval T between the ticks of a clock moving at velocity v is given by T = T′/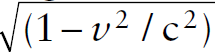 , where T′ is the time interval between ticks of the clock in its own reference frame. At slow speeds v << c, one expands the square root by the Taylor series expansion 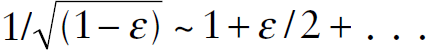to obtain T ~ T′ (1+v²/(2c²)). For satellites orbiting Earth in about 720 minutes, their speed makes the time correction factor about 1.1 × 10^–10. Multiplied by the speed of light, this time factor corresponds to a distance error of about 3.3 centimeters for each second.

From the GTR, the time interval T between clock ticks at radial distance R outside of a body of mass M is given by 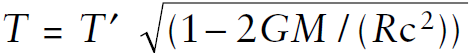. Consider two different radii: r₁ = 6.37 × 10⁶ m and r₂ = 2.02 × 10⁷ m. Substitute the two radii for the two distances from the massive body and take the difference. One calculates a clock correction factor of about 4.8 × 10^–10 for this GTR effect, a little more than four times the STR effect, or about 14.4 centimeters of error every second. So in 10 minutes even this small effect produces an error of about 86 meters if not accounted for. Who would have thought that both STR and GTR effects are big enough to play important roles in such a useful practical system as GPS!