Tea in Thermos

One liter of tea at 90°C is poured into a vacuum-insulated container (thermos). The surface area of the thermos walls A = 600 cm². The volume between the walls is pumped down to P₀ ~ 5 × 10^-6 atm pressure (at room temperature). The emissivity of the walls ϵ = 0.1, and the thermal capacity of water C = 4.2 × 10³ J/kg K. Disregarding the heat leakage through the stopper, estimate the

a) Net power transfer

b) Time for the tea to cool from 90°C to 70°C.

SOLUTION

There are two main sources of power dissipation: radiation from the walls of the thermos and thermal conductance of the air between the walls. Let us first estimate the radiative loss. The power radiated from the hotter inner wall minus the power absorbed from the outer wall is given by

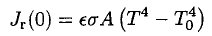  (1)

where T is the temperature of the tea, T₀ is room temperature, and the Stefan–Boltzmann constant σ = 5.7 × 10^-8 W/m²K⁴. Initially, T = 363 K, T₀ = 393 K. So

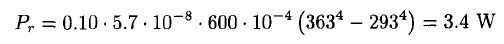
The power dissipation due to the thermal conductivity of the air can be estimated from the fact that, at that pressure, the mean free path of the air molecules is about λ ~ 1 cm. Therefore, there are very few collisions between the molecules that travel from one wall of the thermos to the other. We can assume that we are in the Knudsen regime of λ ≥ d (d is the distance between the walls). In this regime the thermal conductance is proportional to the pressure (if λ << d, it is independent of the pressure). Let us assume that after a molecule strikes the wall, it acquires the temperature of the wall. Initially after it hits the wall, a molecule will take away the energy

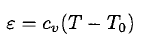(2)

where we can take for air c_v ~ 5/2 k_B. The number of molecules striking the inner wall per time interval dt is

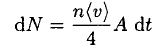(3)

where n is the concentration of molecules and (v) is their average velocity. The power due to the thermal conductance is

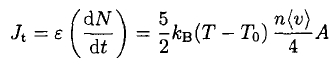(4)

We can substitute n = P/k_BT₀ and

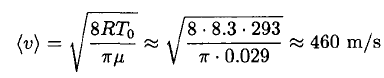
Then (4) becomes

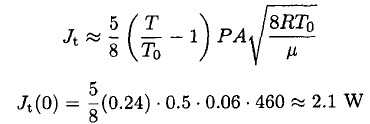(5)

So, we can see that radiation loss has about the same order of magnitude as thermal conductance at these parameters. Therefore the properties of the thermos can only be improved significantly by decreasing both the emissivity and the residual pressure between the walls. The energy dissipated is equal to the energy change of the mass m of the tea:

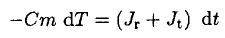(6)

So

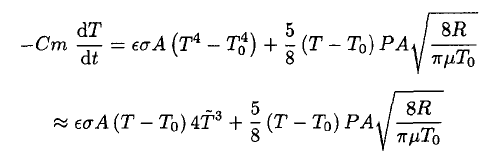(7)

where we used for an estimate the fact that T does not change significantly and 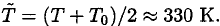 Then the time t for the tea to cool from the initial temperature T_i to the final temperature T_f is given by

(8)