Equipartition Theorem

a) For a classical system with Hamiltonian

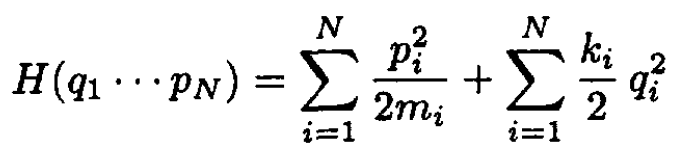
at a temperature τ, show that

b) Using the above, derive the law of Dulong and Petit for the heat capacity of a harmonic crystal.

c) For a more general Hamiltonian,

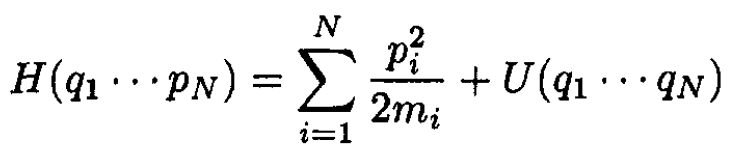
prove the generalized equipartition theorem:

where x₁ = q₁,…, x_N = q_N, x_N+1 = p₁,…,x_2N = p_N. You will need to use the fact that U is infinite at q_i = ±∞.

d) Consider a system of a large number of classical particles and assume a general dependence of the energy of each particle on the generalized coordinate or momentum component q given by ε (q) where

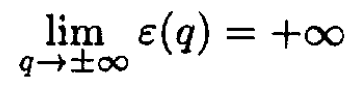
Show that, in thermal equilibrium, the generalized equipartition theorem holds:

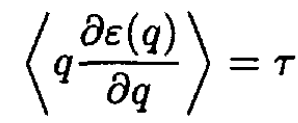
What conditions should be satisfied ε (q)  for to conform to the equipartition theorem?

SOLUTION

a) For both of these averages the method is identical, since the Hamiltonian depends on the same power of either or q. Compose the first average as follows:

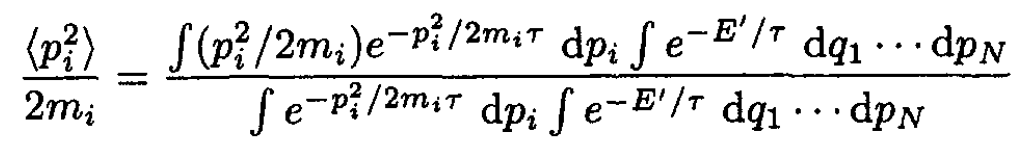(1)

where the energy is broken into the p_i - dependent term and E', the rest of the sum. The second integrals in the numerator and denominator cancel, so the remaining expression may be written

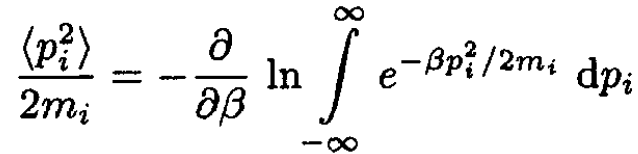(2)

where, as usual, β ≡ 1/τ. A change of variables produces a piece dependent on β and an integral that is not:

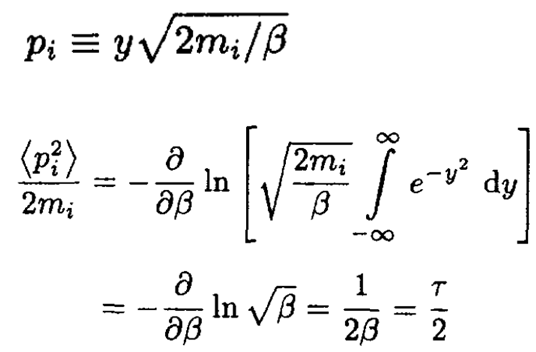(3)

The (k_i/2) ⟨q²_i⟩ average proceeds in precisely the same way, yielding

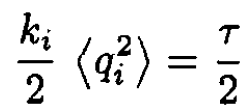(4)

b) The heat capacity, C_V, at constant volume is equal to ∂E/∂τ. From part (a), we have

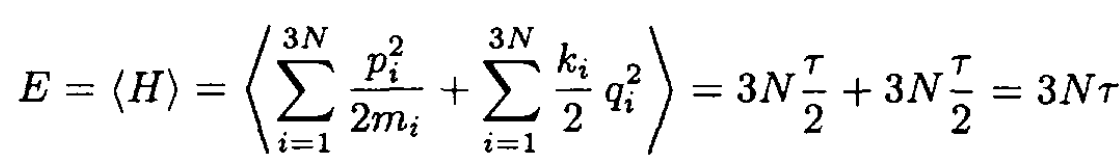(5)

where we now sum over the 3-space and momentum degrees of freedom per atom. The heat capacity,

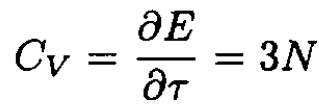(6)

is the law of Dulong and Petit.

c) Now take the average:

(7)

Integration by parts yields

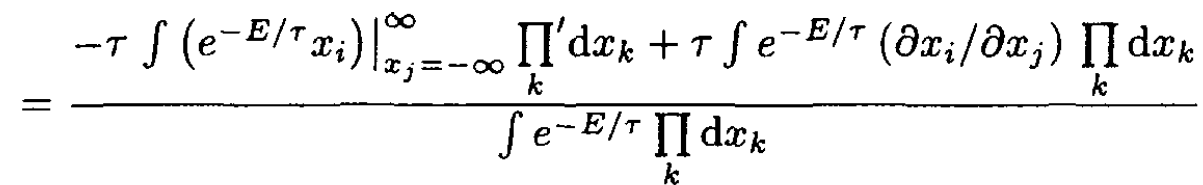(8)

where the prime on the product sign in the first term indicates that we integrate over all x_i except i = j. If i ≠ j, then the first term in the numerator equals zero. If x_j is one of the q's, then by the assumption of U infinite, the term still equals zero. Finally, if i = j > N ,then by l’Hôpital’s rule the first term again gives zero. In the second term, ∂x_i/∂x_j = δ_ij, so the expression reduces to

(9)

Finally,

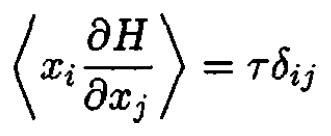(10)

d) By definition,

(11)

Given a polynomial dependence of the energy on the generalized coordinate:

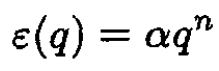(12)

(11) yields

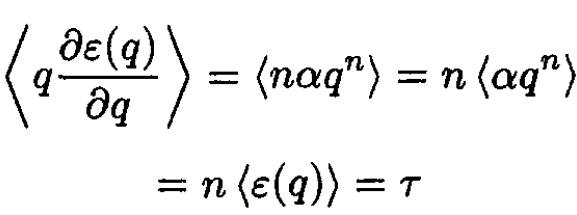(13)

To satisfy the equipartition theorem:

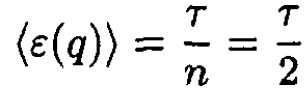(14)

Thus, we should have n = 2.

اخر الاخبار

اخبار العتبة العباسية المقدسة

المجمَع العلمي يطلق الدورة التطويرية الخامسة لمعلمي التربية الإسلامية ومدرسيها في النجف الأشرف

خدمات إنسانية متنوّعة تقدّمها شعبة الشهداء والجرحى في مختلف المحافظات

قسم العلاقات العامة يطلق فعاليات مخيم البذرة الواعدة الخاص بأبناء المنتسبين

جامعة العميد تنظم سلسلة دورات تطويرية لملاكاتها الإدارية

المزيد

الآخبار الصحية

اختراق علمي.. دواء يؤخر ظهور السكري من النوع الأول لسنوات

هذا ما يحدث لجسمك إن أهملت نظافة فراشك

لماذا تعتبر النساء أكثر عرضة للإصابة بألزهايمر من الرجال؟

لماذا يحذر الخبراء من الإفراط في تناول الفراولة؟

المزيد

الآخبار التكنلوجية

السيارات الكهربائية أنظف بنسبة 73% من سيارات الوقود

سيارة لوسِد الكهربائية تدخل "غينيس" بأطول مدى في العالم

نظرية جديدة تنسف كل ما نعرفه عن تشكل أول قارة في الأرض

منذ 37 ألف عام.. دراسة تكشف "أقدم أمراض" أصابت البشر

المزيد

مواضيع ذات صلة

جسيمات التماثل الفائق الفوتينوات ، سكواركات ..المادة الظل.. الأكسيونات ..إلخ .

ريادةالانسان للفضاء -قدرة الله في خلق الطيور(كيف الهمت الطيور الانسان )

التجريبية المنطقية وميكانيكا الكم: رؤية كاسيرر بين العلم والفلسفة

المفاهيم الفيزيائية بين الدقة العلمية والتأويل الفلسفي

"توحيد العلوم عبر استبعاد الميتافيزيقا

إرنست ماخ: توحيد الفيزياء عبر الإدراكات الحسية واستبعاد الميتافيزيقا

"الفيزياء بين الكلاسيكية والكم: من حتمية الأشياء إلى نسبية القوانين"

قوانين البقاء في الفيزياء The Conservation Laws of Physics

من كاسيرر إلى ميكانيكا الكم: تطور مفهوم السببية في الفيزياء والفلسفة

نظرة فلسفية لميكانيكا الكم: هل يمكن فهم الحياة بمفاهيم الفيزياء؟

الطول والزمن في النسبية: التحدي الفيزيائي للفلسفة التقليدية

نسبية الطول بين الفيزياء والفلسفة: أينشتاين في مواجهة فالين