
Einstein Specific Heat
 المؤلف:
Sidney B. Cahn, Gerald D. Mahan And Boris E. Nadgorny
المؤلف:
Sidney B. Cahn, Gerald D. Mahan And Boris E. Nadgorny
 المصدر:
A GUIDE TO PHYSICS PROBLEMS
المصدر:
A GUIDE TO PHYSICS PROBLEMS
 الجزء والصفحة:
part 2 , p 46
الجزء والصفحة:
part 2 , p 46
 26-8-2016
26-8-2016
 1822
1822
Einstein Specific Heat
a) Derive an expression for the average energy at a temperature τ of a quantum harmonic oscillator having natural frequency ω.
b) Assuming unrealistically (as Einstein did) that the normal-mode vibrations of a solid all have the same natural frequency (call it ωE), find an expression for the heat capacity of an insulating solid.
c) Find the high-temperature limit for the heat capacity as calculated in (b) and use it to obtain a numerical estimate for the heat capacity of a V = 5 cm3 piece of an insulating solid having a number density of n = 6 × 1028 atoms/m3. Would you expect this to be a poor or a good estimate for the high-temperature heat capacity of the material? Please give reasons.
d) Find the low-temperature limit of the heat capacity and explain why it is reasonable in terms of the model.
SOLUTION
a) For a harmonic oscillator with frequency ω the energy
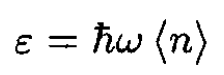 (1)
(1)
where
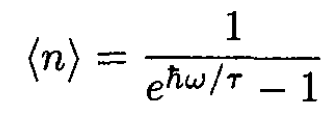
So,
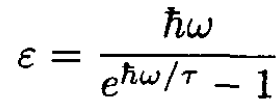 (2)
(2)
b) If we assume that the N atoms of the solid each have three degrees of freedom and the same frequency ωE, then the total energy
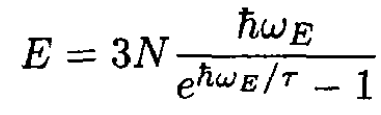 (3)
(3)
The specific heat
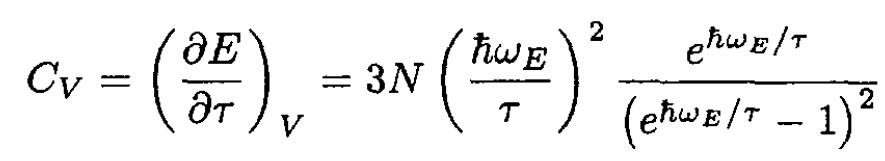 (4)
(4)
c) In the high-temperature limit of (4) (hωE << τ), we have
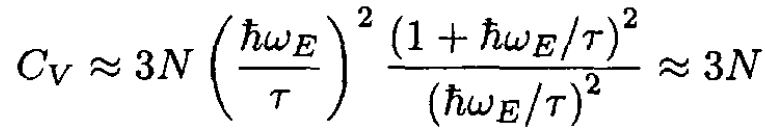 (5)
(5)
In regular units
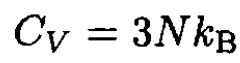
which corresponds to the law of Dulong and Petit, does not depend on the composition of the material but only on the total number of atoms and should be a good approximation at high temperatures, especially for one-component elements. Prom the numbers in the problem,
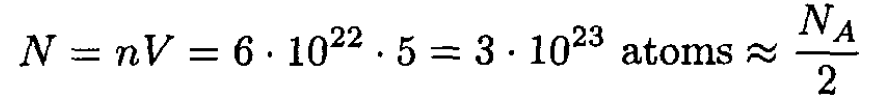 (6)
(6)
Therefore,
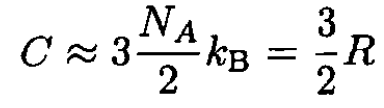 (7)
(7)
Note that, at high enough temperatures. Anharmonic corrections are usually negative and linearly proportional to temperature.
d) At low temperatures (4) becomes
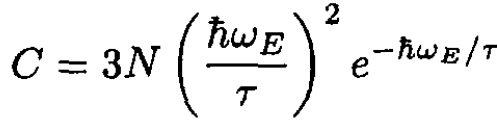 (8)
(8)
The heat capacity goes to zero as exp (-hωE/τ) at τ → 0, whereas the experimental results give 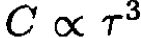 . The faster falloff of the heat capacity is due to the “freezing out” of the oscillations at τ → 0 given the single natural frequency ωE.
. The faster falloff of the heat capacity is due to the “freezing out” of the oscillations at τ → 0 given the single natural frequency ωE.
 الاكثر قراءة في مواضيع اخرى
الاكثر قراءة في مواضيع اخرى
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة


