
Dark Matter
 المؤلف:
Sidney B. Cahn, Gerald D. Mahan And Boris E. Nadgorny
المؤلف:
Sidney B. Cahn, Gerald D. Mahan And Boris E. Nadgorny
 المصدر:
A GUIDE TO PHYSICS PROBLEMS
المصدر:
A GUIDE TO PHYSICS PROBLEMS
 الجزء والصفحة:
part 2 , p 38
الجزء والصفحة:
part 2 , p 38
 25-8-2016
25-8-2016
 1624
1624
Dark Matter
From virial theorem arguments, the velocity dispersions of bright stars in dwarf elliptical galaxies imply that most of the mass in these systems is in the form of “dark” matter - possibly massive neutrinos (see Figure 1.1). The central parts of the Draco dwarf galaxy may be modeled as an isothermal gas sphere, with a phase-space distribution of mass of the form
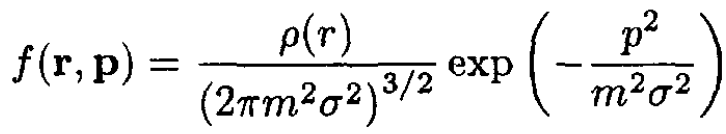
Here, ρ(r) is the local mass density in the galaxy, σ is the velocity dispersion, and m is the mass of a typical “particle” in the galaxy. Measurements on Draco yield  light years). r0 is the “core” radius, where the density has decreased by close to a factor of 2 from its value at r = 0.
light years). r0 is the “core” radius, where the density has decreased by close to a factor of 2 from its value at r = 0.
a) Using the virial theorem, write a very rough (order of magnitude) relation between r0, σ, and ρ(0).
b) Assume that most of the mass in Draco resides in one species of massive neutrino. Show how, if the Pauli exclusion principle is not to be violated, the distribution function above sets a lower limit on the mass of this neutrino.
c) Using the observations and the result of part (a), estimate this lower limit (in units of eV/c2) and comment on whether current measurements of neutrino masses allow Draco to be held together in the manner suggested.

Figure 1.1
SOLUTION
a) The virial theorem may be written relating the average kinetic energy, ⟨T⟩, and the forces between particles:
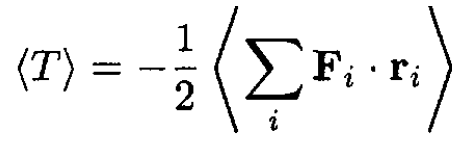
For an inverse square law force (gravitation), the average kinetic energy ⟨T⟩ and potential energy ⟨U⟩ are related as
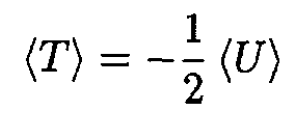 (1)
(1)
For a very rough estimate of the gravitational potential energy of Draco, consider the energy of a sphere of uniform density ρ(0) and radius r0:
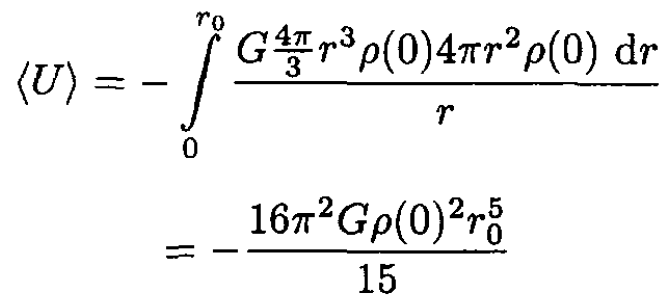 (2)
(2)
The average kinetic energy may be approximated by
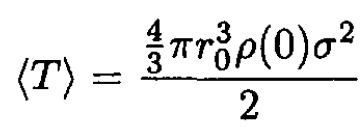 (3)
(3)
Substituting (2) and (3) into (1), we find
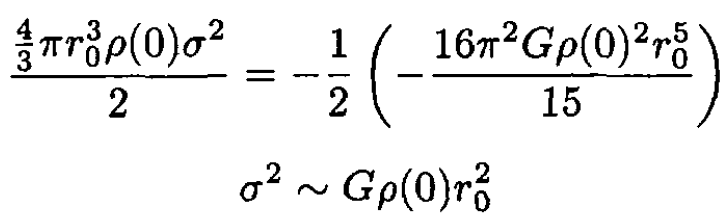 (4)
(4)
b) If most of the mass of Draco is in massive neutrinos, we may estimate the energy by considering the energy of a uniform distribution of fermions in a box of volume V. The energy of such a fermionic gas:
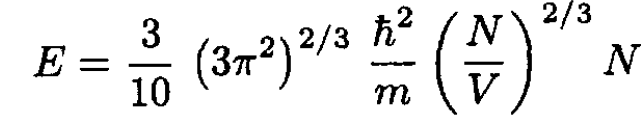 (5)
(5)
Rewriting (5) in terms of density and volume gives
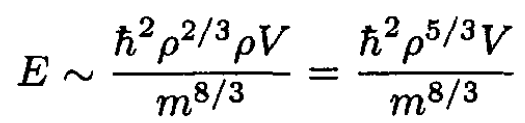 (6)
(6)
If the mass of the neutrino is too low, in order to maintain the observed density, the number density would increase, and the Pauli principle would require the kinetic energy to increase. So, in (6), the energy increases as the mass of the neutrino decreases. Equating the kinetic energy from (a) with (6), we see
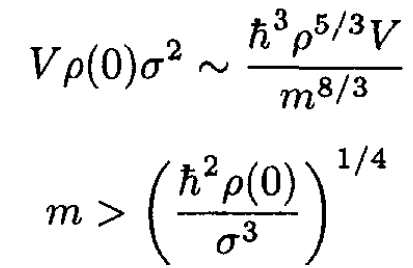 (7)
(7)
c) Substituting (4) into (7), we determine that
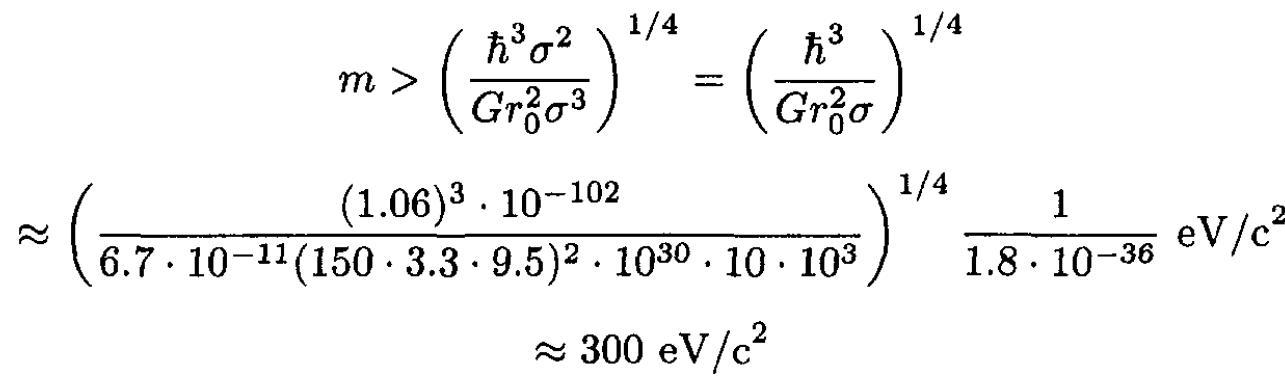
This value is at least an order of magnitude larger than any experimental results for neutrino masses, implying that the model does not explain the manner in which Draco is held together.
 الاكثر قراءة في مواضيع اخرى
الاكثر قراءة في مواضيع اخرى
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة


