


 الفيزياء الكلاسيكية
الفيزياء الكلاسيكية
 الكهربائية والمغناطيسية
الكهربائية والمغناطيسية
 علم البصريات
علم البصريات
 الفيزياء الحديثة
الفيزياء الحديثة
 النظرية النسبية
النظرية النسبية
 الفيزياء النووية
الفيزياء النووية
 فيزياء الحالة الصلبة
فيزياء الحالة الصلبة
 الليزر
الليزر
 علم الفلك
علم الفلك
 المجموعة الشمسية
المجموعة الشمسية
 الطاقة البديلة
الطاقة البديلة
 الفيزياء والعلوم الأخرى
الفيزياء والعلوم الأخرى
 مواضيع عامة في الفيزياء
مواضيع عامة في الفيزياء|
Read More
Date: 11-8-2016
Date: 8-8-2016
Date: 30-8-2016
|
Two Delta Function Potentials
A particle of mass m moves in a one-dimensional potential of the form
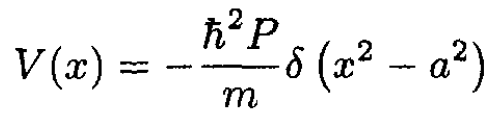 (i)
(i)
where P is a positive dimensionless constant and a has units of length. Discuss the bound states of this potential as a function of P.
SOLUTION
There are two delta function singularities, one at x = a and one at x = -a. The potential can be written in an equivalent way as
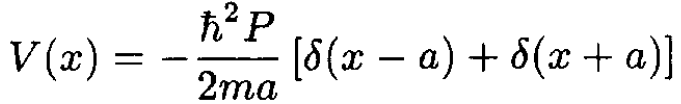 (1)
(1)
At each delta function we match the amplitudes of the eigenfunctions as well as the slopes, using a relation such as (3). A single, isolated, attractive, professional, delta function potential has a single bound state. We expect that a pair of delta function potentials will generally have one or two bound states.
The lowest energy state, for symmetric potentials, is a symmetric eigenfunction. The eigenvalue has the form E = -h2α2/2m, where α is the decay constant of the eigenfunction. The most general symmetric eigenfunction for a bound state is
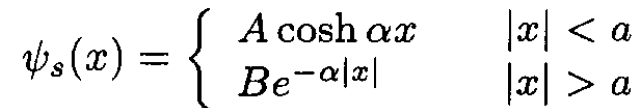 (2)
(2)
Matching at either x = ±a gives the pair of equations:
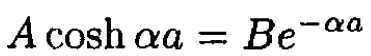 (3)
(3)
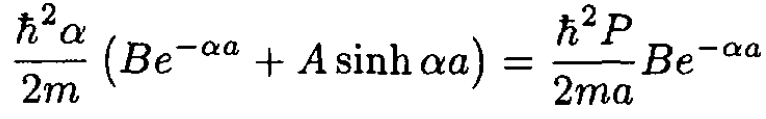 (4)
(4)
Eliminating the constants A and B gives the final equation for the unknown constant α:
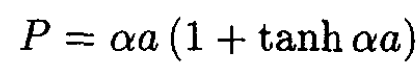 (5)
(5)
For large values of αa the hyperbolic tangent is unity, and we have the approximate result that P ≈ 2αa, which gives for large P the eigenvalue E ≈ -h2P2/8ma2. For small values of αa we see that P ≈ αa and E ≈ -h2P2/2ma2 This is always the lowest eigenvalue.
The other possible eigenstate is antisymmetric: it has odd parity. When the separate bound states from the two delta functions overlap, they combine into bonding and antibonding states. The bonding state is the symmetric state we calculated above. Now we calculate the antibonding state, which is antisymmetric:
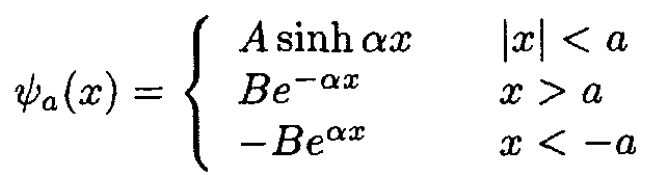 (6)
(6)
Using the same matching conditions, we find the two equations, which are reduced to the final equation for α:
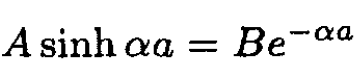 (7)
(7)
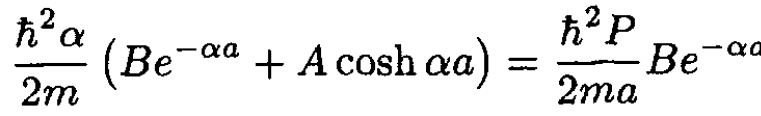 (8)
(8)
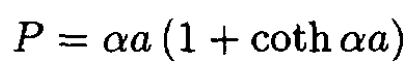 (9)
(9)
For large values of αa the hyperbolic cotangent function (coth) approaches unity, and again we find P ≈ αa and E ≈ -h2P2/8ma2. At small values of x the factor of x coth x → 1. Here we have x = αa, so we find at small values of αa that P → 1. The antisymmetric mode only exists for P > 1. For P < 1 the only bound state is the symmetric one. For P > 1 there are two bound states, symmetric and antisymmetric.



|
|
|
|
علامات بسيطة في جسدك قد تنذر بمرض "قاتل"
|
|
|
|
|
|
|
أول صور ثلاثية الأبعاد للغدة الزعترية البشرية
|
|
|
|
|
|
|
مدرسة دار العلم.. صرح علميّ متميز في كربلاء لنشر علوم أهل البيت (عليهم السلام)
|
|
|