
Circle with Field
 المؤلف:
Sidney B. Cahn, Gerald D. Mahan And Boris E. Nadgorny
المؤلف:
Sidney B. Cahn, Gerald D. Mahan And Boris E. Nadgorny
 المصدر:
A GUIDE TO PHYSICS PROBLEMS
المصدر:
A GUIDE TO PHYSICS PROBLEMS
 الجزء والصفحة:
part 2 , p 66
الجزء والصفحة:
part 2 , p 66
 14-8-2016
14-8-2016
 1519
1519
Circle with Field
A particle with charge e and mass m is confined to move on the circumference of a circle of radius r. The only term in the Hamiltonian is the kinetic energy, so the eigenfunctions and eigenvalues are
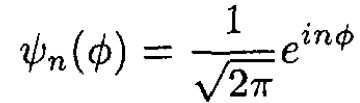 (i)
(i)
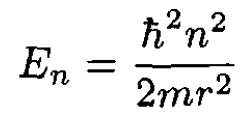 (ii)
(ii)
where ϕ is the angle around the circle. An electric field E is imposed in the plane of the circle. Find the perturbed energy levels up to O(|E|2).
SOLUTION
The perturbation is V(ϕ) = -e|E|r cos ϕ if we assume the field is in the x-direction. The same result is obtained if we assume the perturbation is in the y-direction (V(ϕ) = -e|E|r sin ϕ). In order to do perturbation theory, we need to find the matrix element of the perturbation between different eigenstates. For first-order perturbation theory we need
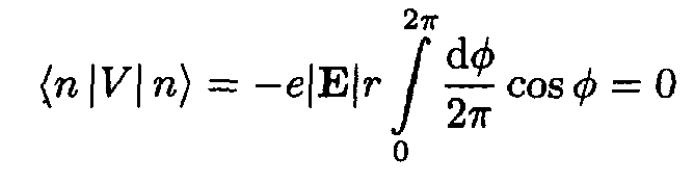 (1)
(1)
The eigenvalues are unchanged to first-order in the field E.
To do second-order perturbation theory, we need off-diagonal matrix elements:
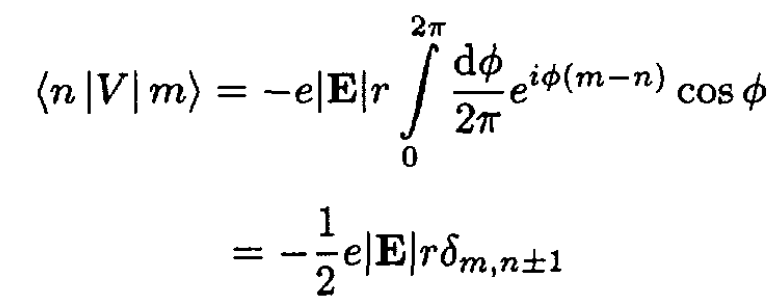 (2)
(2)
If we recall that cos ϕ = (eiϕ + -eiϕ)/2, then we see that n – m can only
equal ±1 for the integral to be nonzero. In doing second-order perturbation
theory for the state |n⟩, the only permissible intermediate states are m = n ± 1:
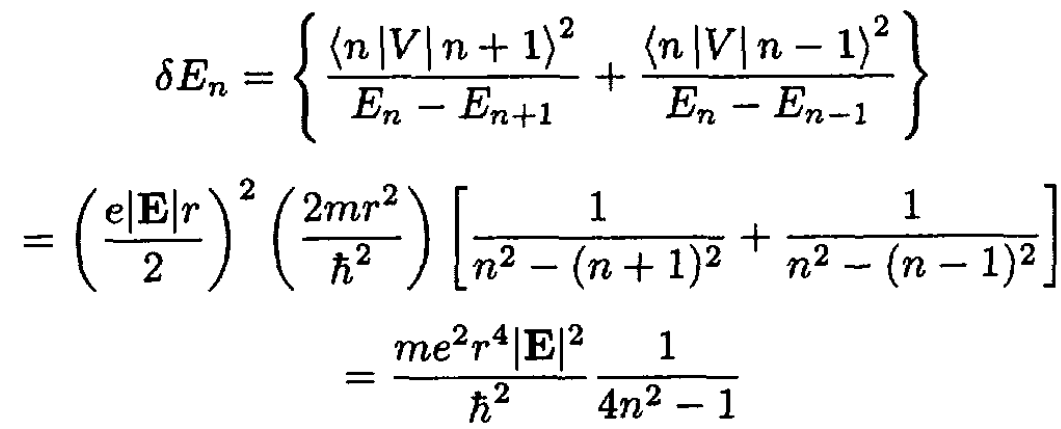 (3)
(3)
This solution is valid for states n > 0. For the ground state, with n = 0, the n – 1, state does not exist, so the answer is
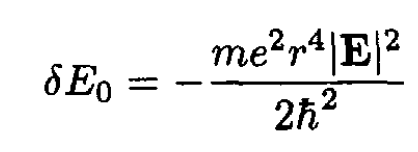 (4)
(4)
 الاكثر قراءة في مواضيع اخرى
الاكثر قراءة في مواضيع اخرى
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة


