
Algebra of Angular Momentum
 المؤلف:
Sidney B. Cahn, Gerald D. Mahan And Boris E. Nadgorny
المؤلف:
Sidney B. Cahn, Gerald D. Mahan And Boris E. Nadgorny
 المصدر:
A GUIDE TO PHYSICS PROBLEMS
المصدر:
A GUIDE TO PHYSICS PROBLEMS
 الجزء والصفحة:
part 2 , p 60
الجزء والصفحة:
part 2 , p 60
 14-8-2016
14-8-2016
 1696
1696
Algebra of Angular Momentum
Given the commutator algebra

a) Show that J2 = J21 + J22 + J23 commutes with J3.
b) Derive the spectrum of {J2, J3} from the commutation relations.
SOLUTION
a)

b) Since J2 and J3 commute, we will try to find eigenstates with eigenvalues of J2 and J3 denoted by |jm⟩ where j, m are real numbers:
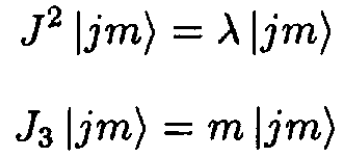
Since J21 + J22 + J23 ≥ J23 we know that λ ≥ m2. Anticipating the result, let λ ≡ j(j + 1). Form the raising and lowering operators J+ and J-:
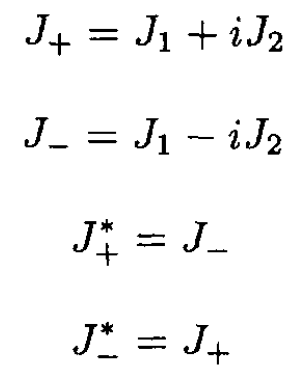
Find the commutators
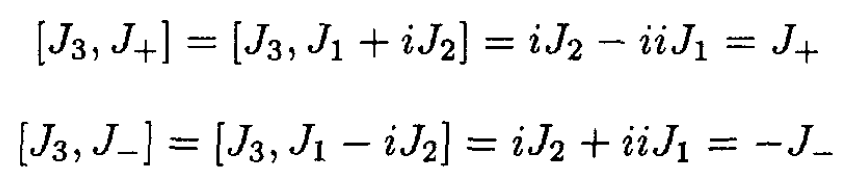 (1)
(1)
From part (a) we know that [J±, J2] = 0. We now ask what is the eigenvalue of J2 for the states J± |jm⟩:
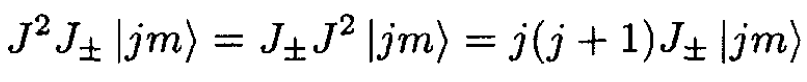 (2)
(2)
So, these states have the same eigenvalue of J2. Now, examine the eigenvalue of J3 for these states:
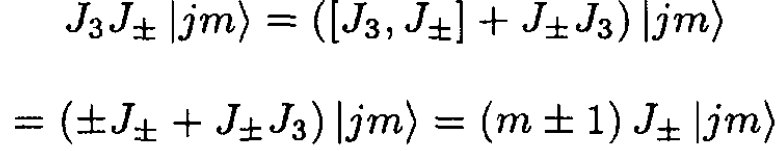 (3)
(3)
In (3) we see that J± has the effect of raising or lowering the m-value of the states |jm⟩ so that
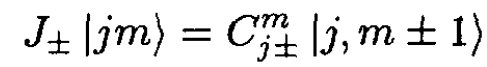
where Cmj± are the corresponding coefficients. As determined above, we know that j(j + 1) ≥ m2, so J± cannot be applied indefinitely to the state |jm⟩; i.e., there must be an m = mmax, m = mmin such that
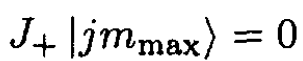 (4)
(4)
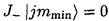 (5)
(5)
Expand J-J+ and apply J- to (4):
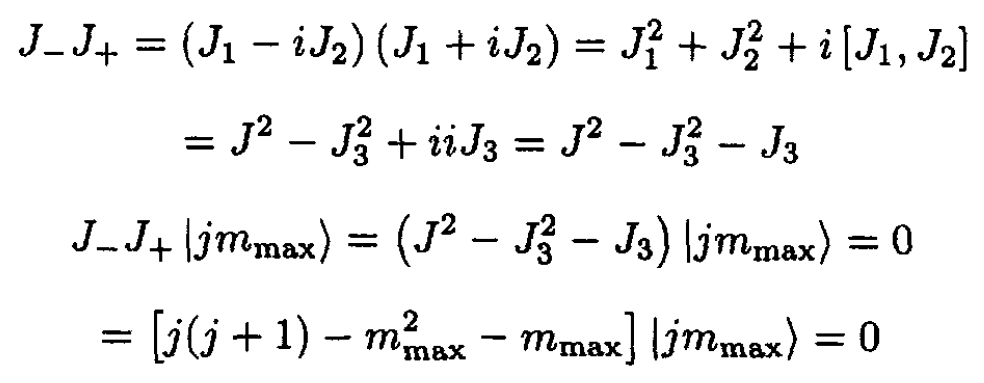
Either the state |jmmax⟩ is zero or j(j + 1) – m2max – mnax = 0. So

Similarly,
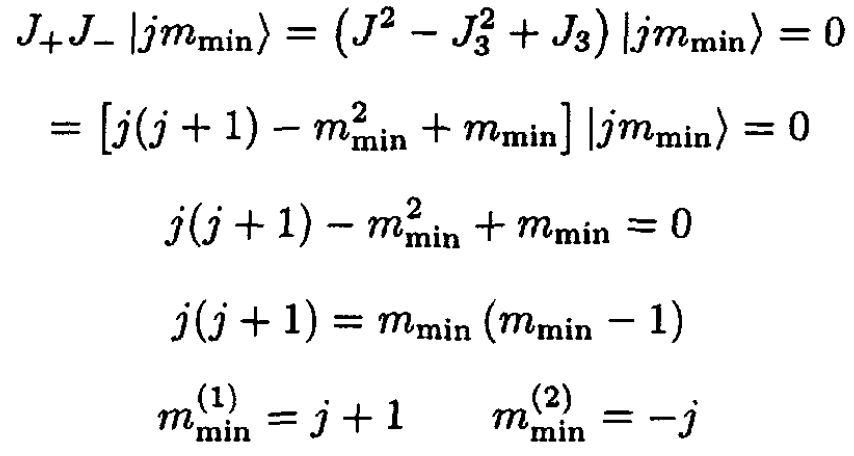
For j ≥ 0, and since mmax ≥ mmin, the only solution is
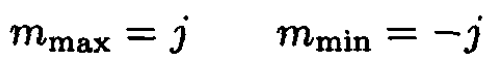
We knew that j was real, but now we have mmax – mmin = 2j = integer, so
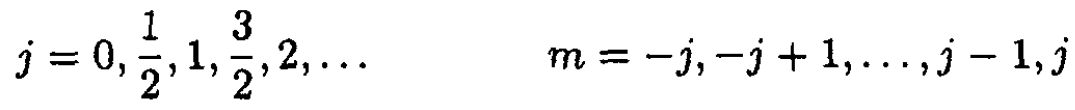
 الاكثر قراءة في مواضيع اخرى
الاكثر قراءة في مواضيع اخرى
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة


