Spherical Resistor

A and B are opposite ends of a diameter AOB of a very thin spherical shell of radius a and thickness t. Current enters and leaves by two small

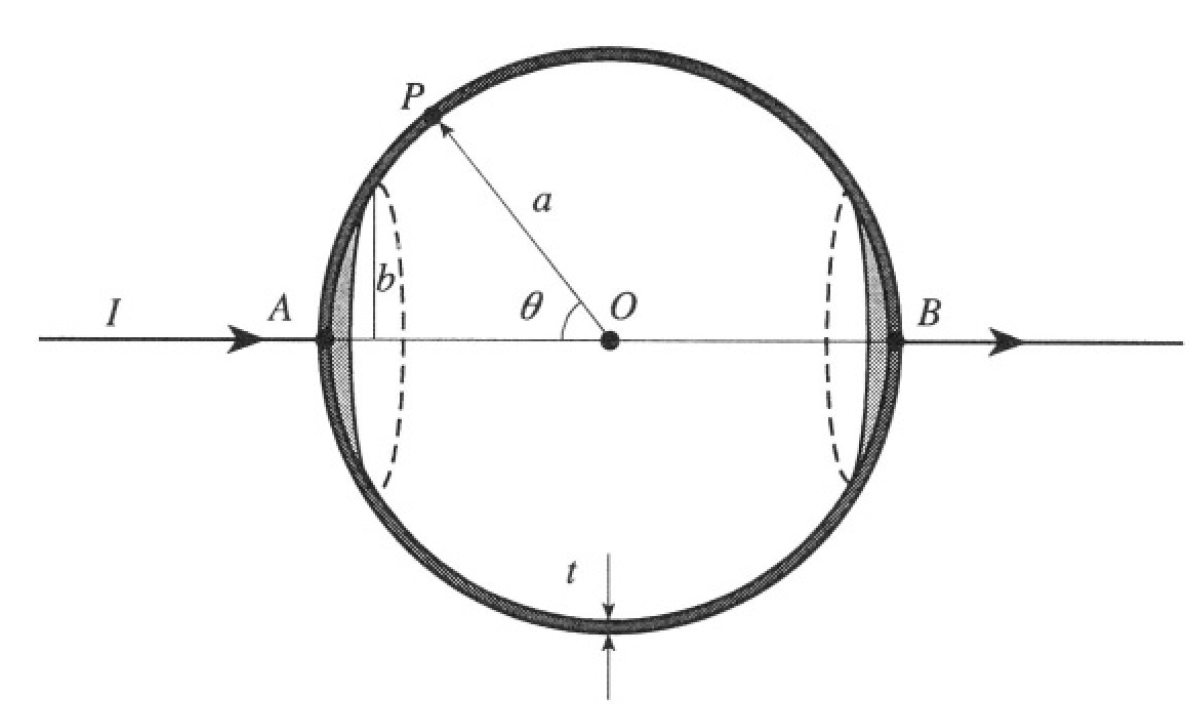
Figure 1.1

circular electrodes of radius b whose centers are at A and B (see Figure 1.1). If I is the total current and P is a point on the shell such that the angle POA = θ, show that the magnitude of the current density vector at P is proportional to (2πat sinθ)^-1. Hence find the resistance of the conductor.

You may find this integral useful:

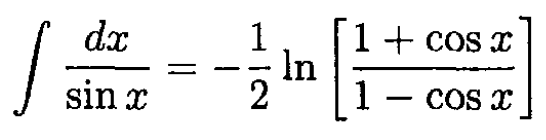
SOLUTION

The current density at point P may be written down immediately because of the cylindrical symmetry of the problem (see Figure 1.2). The current

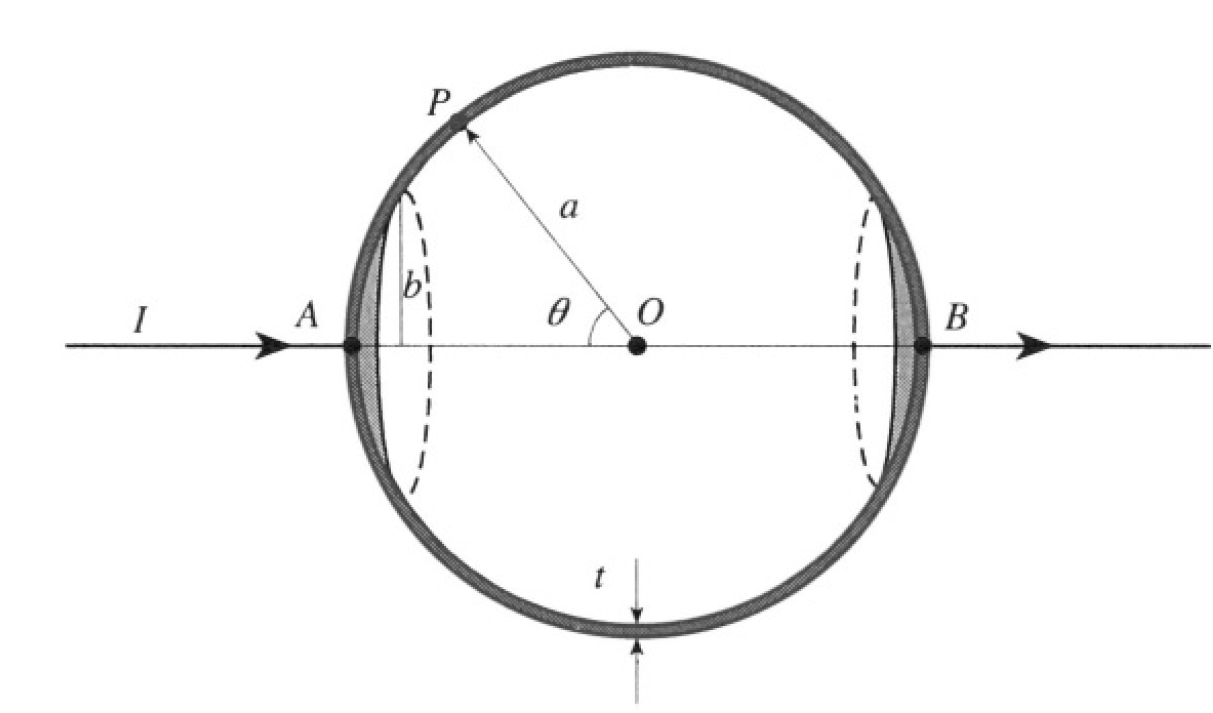
Figure 1.2

 is divided evenly through 2π so that the current density J at each point in the spherical shell is

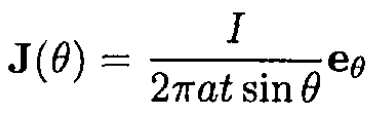(1)

From the equation J = σE, where σ is the conductivity of the shell, we obtain

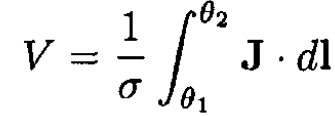
where V is the potential difference between the two electrodes. So

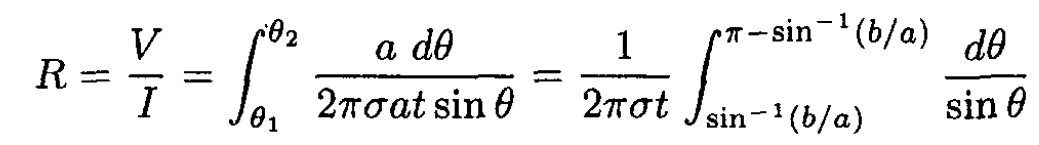(2)

From the hint in the problem (which can by computed by using the substitution tan θ/2 = t) we can take the integral in (2):

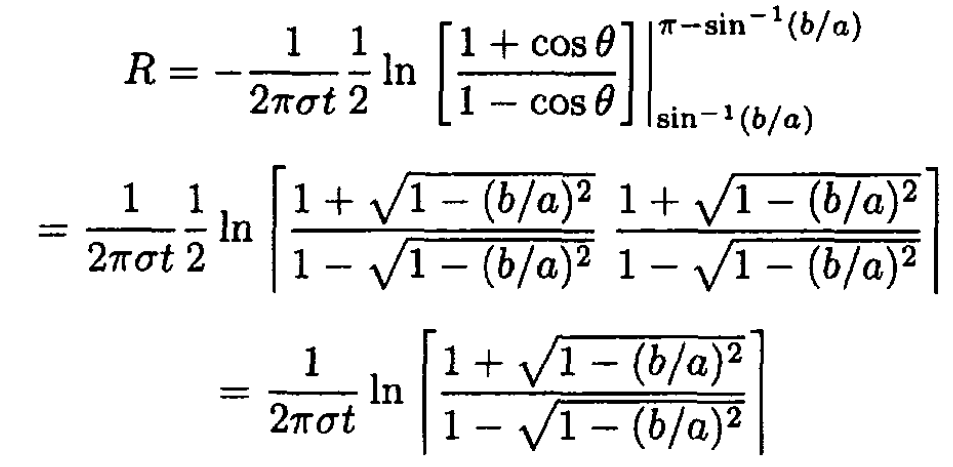
As the radius b of the electrodes goes to zero, the resistance goes to infinity!