
تاريخ الفيزياء

علماء الفيزياء


الفيزياء الكلاسيكية

الميكانيك

الديناميكا الحرارية


الكهربائية والمغناطيسية

الكهربائية

المغناطيسية

الكهرومغناطيسية


علم البصريات

تاريخ علم البصريات

الضوء

مواضيع عامة في علم البصريات

الصوت


الفيزياء الحديثة


النظرية النسبية

النظرية النسبية الخاصة

النظرية النسبية العامة

مواضيع عامة في النظرية النسبية

ميكانيكا الكم

الفيزياء الذرية

الفيزياء الجزيئية


الفيزياء النووية

مواضيع عامة في الفيزياء النووية

النشاط الاشعاعي


فيزياء الحالة الصلبة

الموصلات

أشباه الموصلات

العوازل

مواضيع عامة في الفيزياء الصلبة

فيزياء الجوامد


الليزر

أنواع الليزر

بعض تطبيقات الليزر

مواضيع عامة في الليزر


علم الفلك

تاريخ وعلماء علم الفلك

الثقوب السوداء


المجموعة الشمسية

الشمس

كوكب عطارد

كوكب الزهرة

كوكب الأرض

كوكب المريخ

كوكب المشتري

كوكب زحل

كوكب أورانوس

كوكب نبتون

كوكب بلوتو

القمر

كواكب ومواضيع اخرى

مواضيع عامة في علم الفلك

النجوم

البلازما

الألكترونيات

خواص المادة


الطاقة البديلة

الطاقة الشمسية

مواضيع عامة في الطاقة البديلة

المد والجزر

فيزياء الجسيمات


الفيزياء والعلوم الأخرى

الفيزياء الكيميائية

الفيزياء الرياضية

الفيزياء الحيوية

الفيزياء العامة


مواضيع عامة في الفيزياء

تجارب فيزيائية

مصطلحات وتعاريف فيزيائية

وحدات القياس الفيزيائية

طرائف الفيزياء

مواضيع اخرى
Parallel Plate Capacitor with Solid Dielectric
المؤلف:
Sidney B. Cahn Boris E. Nadgorny
المصدر:
A GUIDE TO PHYSICS PROBLEMS
الجزء والصفحة:
part 1 , p 49
11-8-2016
1712
Parallel Plate Capacitor with Solid Dielectric
Two square metal plates of side L are separated by a distance d << L. A dielectric slab of size L × L × d just slides between the plates. It is inserted a distance x (parallel to one side of the squares) and held there (see Figure
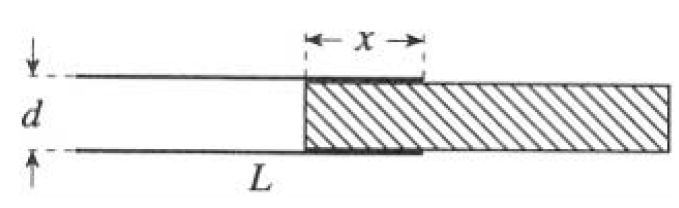
Figure 1.1
1.1). The metal plates are then charged to a potential difference V and disconnected from the voltage source.
a) Find the force exerted electrically on the slab. Be careful and explicit about its direction.
b) How does the situation change if the battery is left connected?
SOLUTION
To solve this problem, the capacitance of a parallel plate capacitor must be calculated with and without a dielectric inserted. We then recognize that the two capacitors are in parallel in order to infer the total capacitance, and we then use the expression for the energy contained in the capacitor to determine the force on the dielectric. The potential difference between the plates is given by
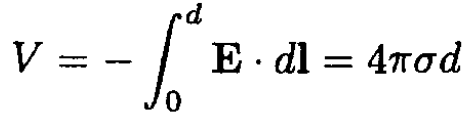 (1)
(1)
where σ is the surface charge density σ = Q/L2. Since Q = CV, we find
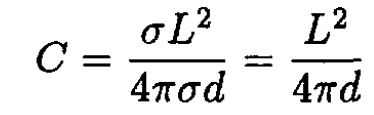 (2)
(2)
a) With a dielectric inserted, the capacitance is modified. E is replaced by D in (1), where D = εE. The potential V is still the integral of –E . dl, so we find that the capacitance is multiplied by ε. In this problem, the dielectric is inserted only a distance x between the plates (see Figure 1.2).
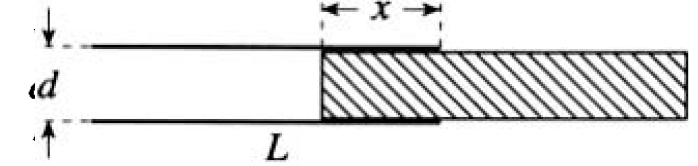
Figure 1.2
As the total capacitance of two capacitors in parallel is simply the sum of the individual capacitances, we find that the new capacitance is
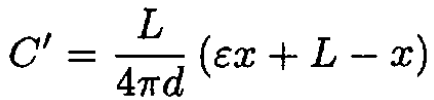 (3)
(3)
The energy stored in a capacitor is given by
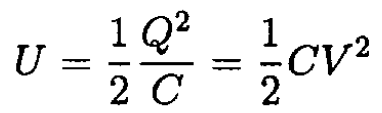 (4)
(4)
In (a), the battery has been disconnected from the capacitor. As the dielectric moves either into or out of the capacitor, the potential V will change while the charge Q is constant. So we use the first part of (4). The force on the dielectric is found from
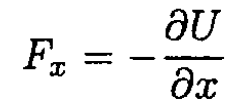 (5)
(5)
From (3) and (4) we have
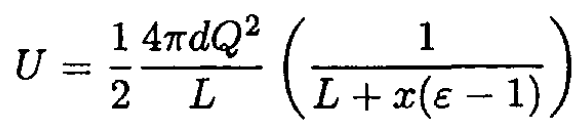
so
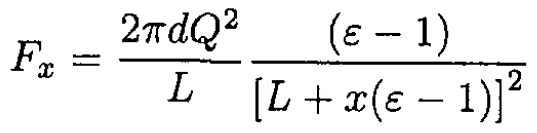 (6)
(6)
Expressing Fx in terms of a potential difference V
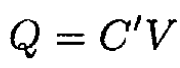
we obtain
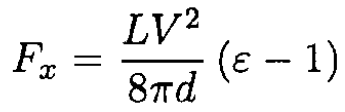
Since ε > 1, the dielectric slab will be drawn further between the plates (x will increase).
b) In this case, V is constant, not Q, and we must now take into account the electric potential energy of the battery. For some small change of the system,
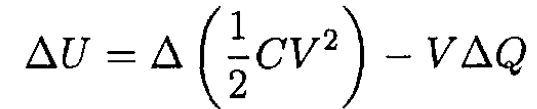
Since Q = CV, and the potential is held fixed ∆Q = V ∆C, so
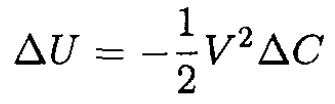
Note the minus sign. If the electric potential energy of the battery had been ignored, the expression would be incorrect. We now wish to find
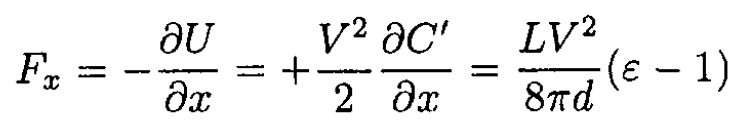 (7)
(7)
as obtained in (a). Note that the force goes to zero when ε = 1, as expected.
 الاكثر قراءة في مواضيع اخرى
الاكثر قراءة في مواضيع اخرى
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة

الآخبار الصحية















 قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة
قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة "المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة
"المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة (نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)
(نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)


















