Not-so-concentric Spherical Capacitor

An insulated metal sphere of radius a with total charge q is placed inside a hollow grounded metal sphere of radius b. The center of the inner sphere is slightly displaced from the center of the outer sphere so that the distance between the two centers is δ (see Figure 1.1).

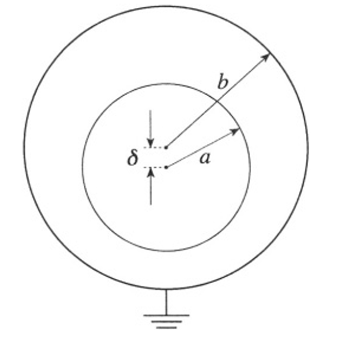
Figure 1.1

a) Use the boundary conditions to determine the potential between the spheres in the case δ = 0.

b) Find the charge distribution of the inner sphere and the force acting on it.

Hint: Show that R(θ) ≈ b + δ cosθ where R is the distance from the center of the inner sphere to the surface of the outer sphere, and write down an expansion for the potential between the spheres using spherical harmonics to first order in δ.

SOLUTION

a) For δ = 0, we have the boundary conditions

(1)

which with Gauss’s law yield for the potential between a and b

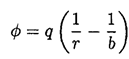
(2)

b) Introduce spherical coordinates with the polar axis along the line (see Figure 1.2). Find the equation of the sphere S_B in these coordinates.

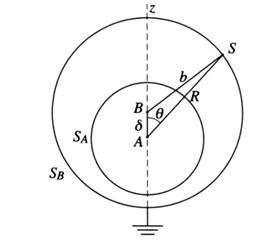
Figure 1.2

From the triangle ∆ABS we have

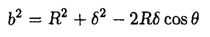
We can expand 1/b as a sum of spherical harmonics using a general formula:

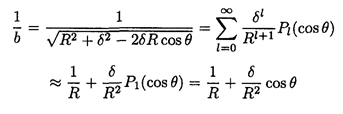
or simply by expanding the square root to first order in δ(δ << R)

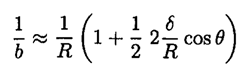
So

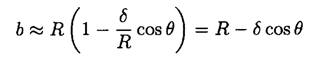
and we have

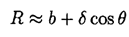
(3)

The term δP₁ (cosθ) represents the deviation from concentricity and should be zero at δ = 0. We look for a potential as an expansion of spherical harmonics to first order in δ

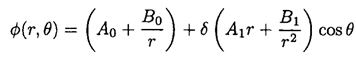
(4)

With the boundary conditions in (1)

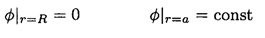
The first term in (4) should be the same as in (a)

We may find A₁ and B₁ by checking the potential on the inner and outer spheres. On the inner sphere r = a and the potential is a constant, and so must be independent of cosθ. This yields

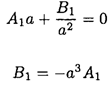
(5)

Substituting (5) back into (4), we now check the potential on the outer sphere, where r = b + δ cosθ

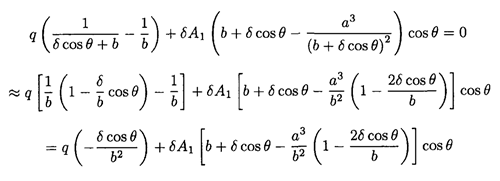
Neglecting terms of order δ², we find

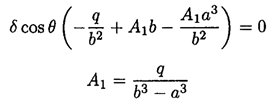
Finally,

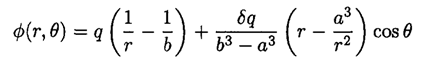
The charge density on the inner sphere is

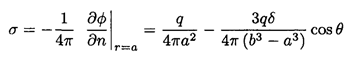
The force on the sphere may now be calculated by integrating the z component of the force on the differential areas of the surface dF = 2πσ²n dA:

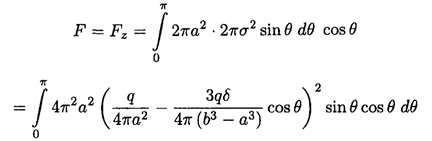
The only term which survives is the cross term

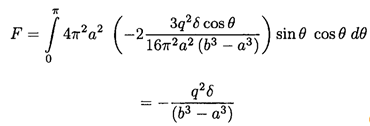
(6)

We can check this result in the limit of a = 0 against the force between a charge inside a neutral sphere and the sphere.