
Current in Wire and Poynting Vector
 المؤلف:
Sidney B. Cahn Boris E. Nadgorny
المؤلف:
Sidney B. Cahn Boris E. Nadgorny
 المصدر:
A GUIDE TO PHYSICS PROBLEMS
المصدر:
A GUIDE TO PHYSICS PROBLEMS
 الجزء والصفحة:
part 1 , p 63
الجزء والصفحة:
part 1 , p 63
 8-8-2016
8-8-2016
 2056
2056
Current in Wire and Poynting Vector
A long straight wire of radius carries a current I in response to a voltage V between the ends of the wire.
a) Calculate the Poynting vector S for this DC voltage.
b) Obtain the energy flux per unit length at the surface of the wire. Compare this result with the Joule heating of the wire and comment on the physical significance.
SOLUTION
a) Let us calculate the flux of the Poynting vector. Introduce cylindrical coordinates with unit vectors eρ, eθ, and ẑ. Current flows along the wire in the z direction and the electric field E = Eẑ. Using one of Maxwell’s equations in vacuum, the fact that conditions are stationary, and Stokes’ theorem,
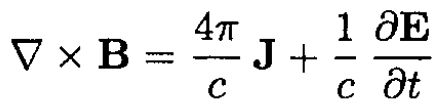 (1)
(1)
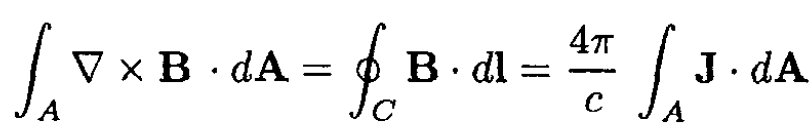 (2)
(2)
where J is the current density and A is the surface. At any given radius r, Bθ is constant, so we have
 (3)
(3)
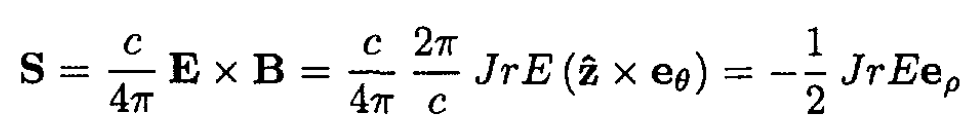 (4)
(4)
Using the relation between current density and total current J = I/(πb2):

b) The Poynting flux per unit length is then S . 2πb = -IE. So the flux enters the wire, and we see that the dissipated power per unit length IE is equal to the total incoming S-flux, in agreement with Poynting’s theorem:
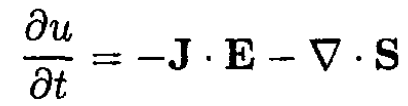 (5)
(5)
where u is the energy density. Under stationary conditions such as ours
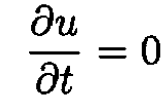
and we have
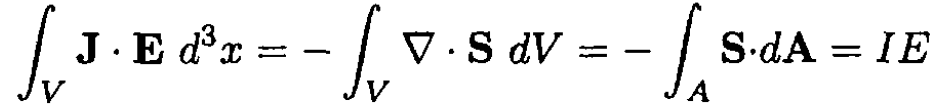
 الاكثر قراءة في مواضيع اخرى
الاكثر قراءة في مواضيع اخرى
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة


