Swan and Crawfish

Two movers, Swan and Crawfish, from Swan, Crawfish, and Pike, Inc., must move a long, low, and narrow dresser along a rough surface with a coefficient of friction μ = 0.5 (see Figure 1.1). The mass M of the dresser is 150 kg. Swan can apply a maximum force of 700 N, and Crawfish 350 N.

 Figure 1.1

Obviously, together they can move the dresser; however, each of them insists on his own way of moving the darn thing, and they cannot agree. Show that by using his own method, each of them can move the dresser alone. What are these methods?

Hint: The names in the problem are not quite coincidental, and the two methods are natural for Swan and Crawfish.

SOLUTION

First consider the method most likely suggested by Swan. Ignorant of the law of gravitational attraction, he does not have to apply a strictly horizontal force, and although the horizontal projection of the force is smaller, the friction is also smaller. Let us assume that he applies the force at the center of mass of the dresser and at an angle α to the horizontal (see Figure 1.2a). Then we can write, for the normal force N exerted by the floor on

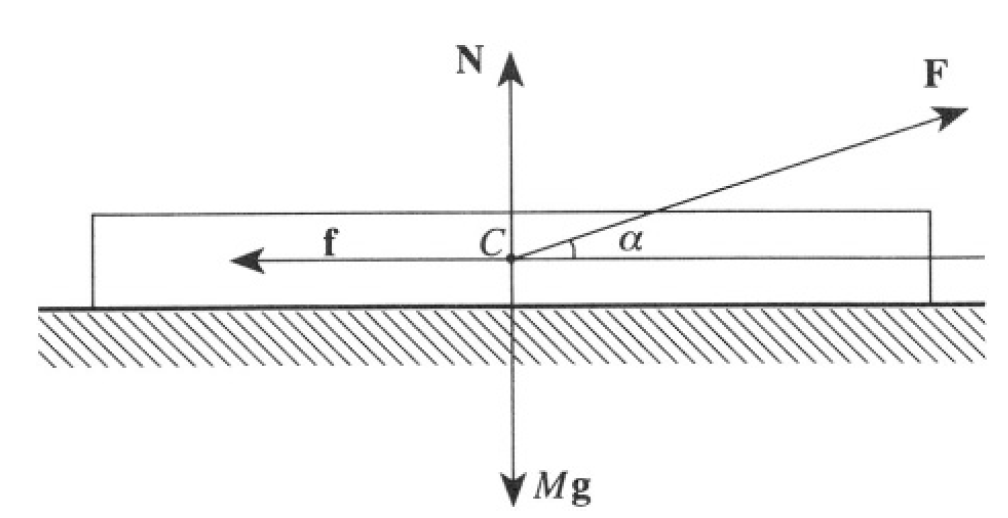
Figure 1.2a

the dresser,

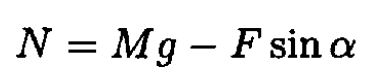
To move the dresser, Swan needs to apply a force F such that its horizontal projection is larger than the friction force

f = μN:

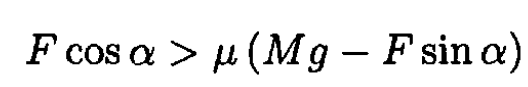
or

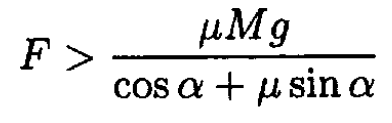(1)

It is easy to check that tan α = μ corresponds to the maximum of the denominator in (1) and therefore to a minimum force F. Using 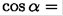 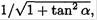 we have

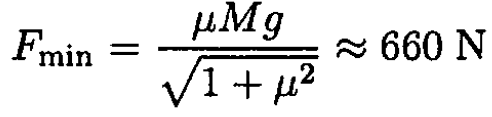
Therefore, the force F should be

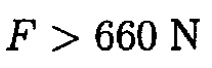
So Swan, who can apply a force of 700 N, will be able to move the dresser alone.

Crawfish, being somewhat more earthbound, is likely to suggest another method of moving the piece of furniture. He will apply a horizontal force, but not to the center of mass of the dresser; rather, to one of its ends. The dresser will start to rotate; however, the center of rotation R will not coincide with the center of mass of the dresser (see Figure 1.2b). So, after one rotation of 180°, Crawfish will have moved the dresser by l-2x, where

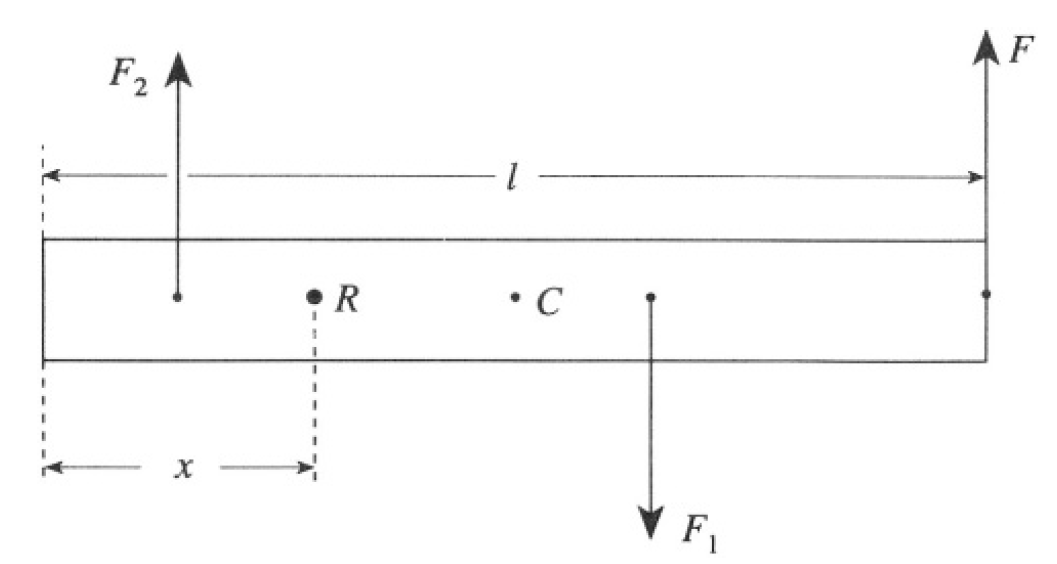
 Figure 1.2b

l is the total length of the dresser. The frictional forces on each of the two parts are F₁ and F₂. They are proportional to the weight of the two parts:

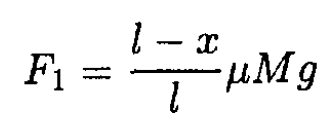(2)

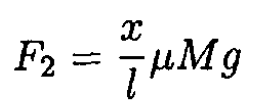 (3)

Since the torque relative to the point R is zero, we have

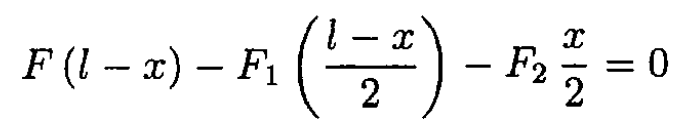
Taking F₁ and F₂ from (2) and (3), we obtain the relation between F and x:

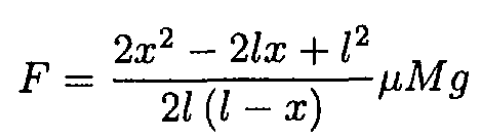
The minimum force F occurs when

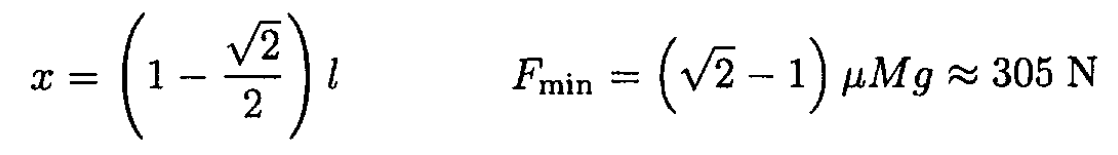
So, Crawfish is also able to move the dresser by his method.