
تاريخ الفيزياء

علماء الفيزياء


الفيزياء الكلاسيكية

الميكانيك

الديناميكا الحرارية


الكهربائية والمغناطيسية

الكهربائية

المغناطيسية

الكهرومغناطيسية


علم البصريات

تاريخ علم البصريات

الضوء

مواضيع عامة في علم البصريات

الصوت


الفيزياء الحديثة


النظرية النسبية

النظرية النسبية الخاصة

النظرية النسبية العامة

مواضيع عامة في النظرية النسبية

ميكانيكا الكم

الفيزياء الذرية

الفيزياء الجزيئية


الفيزياء النووية

مواضيع عامة في الفيزياء النووية

النشاط الاشعاعي


فيزياء الحالة الصلبة

الموصلات

أشباه الموصلات

العوازل

مواضيع عامة في الفيزياء الصلبة

فيزياء الجوامد


الليزر

أنواع الليزر

بعض تطبيقات الليزر

مواضيع عامة في الليزر


علم الفلك

تاريخ وعلماء علم الفلك

الثقوب السوداء


المجموعة الشمسية

الشمس

كوكب عطارد

كوكب الزهرة

كوكب الأرض

كوكب المريخ

كوكب المشتري

كوكب زحل

كوكب أورانوس

كوكب نبتون

كوكب بلوتو

القمر

كواكب ومواضيع اخرى

مواضيع عامة في علم الفلك

النجوم

البلازما

الألكترونيات

خواص المادة


الطاقة البديلة

الطاقة الشمسية

مواضيع عامة في الطاقة البديلة

المد والجزر

فيزياء الجسيمات


الفيزياء والعلوم الأخرى

الفيزياء الكيميائية

الفيزياء الرياضية

الفيزياء الحيوية

الفيزياء والفلسفة

الفيزياء العامة


مواضيع عامة في الفيزياء

تجارب فيزيائية

مصطلحات وتعاريف فيزيائية

وحدات القياس الفيزيائية

طرائف الفيزياء

مواضيع اخرى
Rotating Pendulum
المؤلف:
Sidney B. Cahn Boris E. Nadgorny
المصدر:
A GUIDE TO PHYSICS PROBLEMS
الجزء والصفحة:
part 1 , p 19
1-8-2016
1996
Rotating Pendulum
The bearing of a rigid pendulum of mass m is forced to rotate uniformly with angular velocity ω (see Figure 1.1). The angle between the rotation
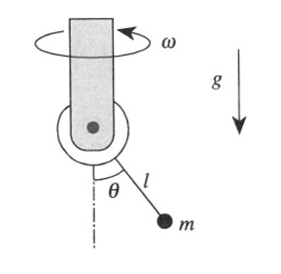
Figure 1.1
axis and the pendulum is called θ. Neglect the inertia of the bearing and of the rod connecting it to the mass. Neglect friction. Include the effects of the uniform force of gravity.
a) Find the differential equation for θ.
b) At what rotation rate ωc does the stationary point at θ = 0 become unstable?
c) For ω > ωc what is the stable equilibrium value of θ?
d) What is the frequency Ω of small oscillations about this point?
SOLUTION
We may compute the Lagrangian by picking two appropriate orthogonal coordinates θ and φ, where equals a constant (see Figure 1.2).
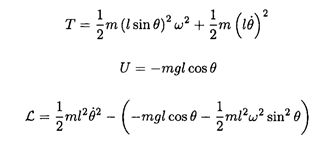
where we consider Ueff = -(1/2) ml2ω2 sin2θ - mgl cos θ.
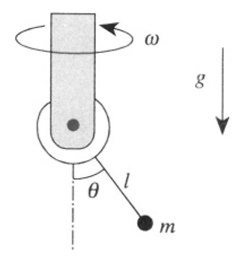
=Figure 1.2
a) Employing the usual Lagrange equations

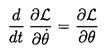
we have
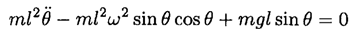
 (1)
(1)
b) (1) has stationary points where ∂Ueff/∂θ = 0.

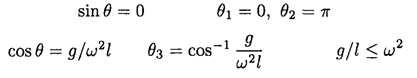
To check these points for stability, take the second derivative
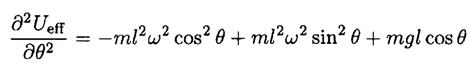 (2)
(2)
At θ = 0 (2) becomes

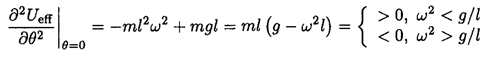
So at angular velocities 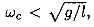
the potential energy has a minimum and the θ = 0 equilibrium point is stable. However at

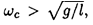 this point is no longer stable. At θ = π:
this point is no longer stable. At θ = π:
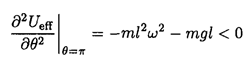

This point is unstable for all values of ω.
c) At 
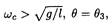 (2) becomes
(2) becomes
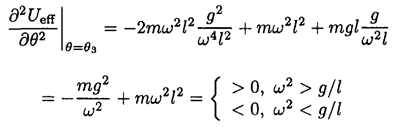

So, here at 
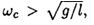 the equilibrium point is stable.
the equilibrium point is stable.
d) Consider the initial differential equation (1) and substitute for θ, θ → θ3+ δ, where θ3 = cos-1(g/ω2):

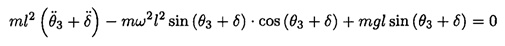
For small oscillations, we will use the approximations sin δ = δ, cos δ = 1-(1/2)δ2 and leave only terms linear in δ:

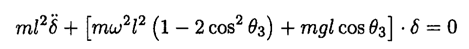
After substituting cos θ3 = g/lω2, we will have for the frequency Ω of small oscillations about this point

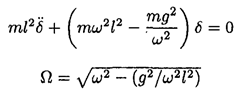
 الاكثر قراءة في مواضيع اخرى
الاكثر قراءة في مواضيع اخرى
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة

الآخبار الصحية















 قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة
قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة "المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة
"المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة (نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)
(نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)


















