
Pulling Strings
 المؤلف:
Sidney B. Cahn Boris E. Nadgorny
المؤلف:
Sidney B. Cahn Boris E. Nadgorny
 المصدر:
A GUIDE TO PHYSICS PROBLEMS
المصدر:
A GUIDE TO PHYSICS PROBLEMS
 الجزء والصفحة:
part 1 , p 8
الجزء والصفحة:
part 1 , p 8
 1-8-2016
1-8-2016
 1759
1759
Pulling Strings
A mass m is attached to the end of a string. The mass moves on a frictionless table, and the string passes through a hole in the table (see Figure 1.1), under which someone is pulling on the string to make it taut at all times. Initially, the mass moves in a circle, with kinetic energy E0. The string is then slowly pulled, until the radius of the circle is halved. How much work was done?
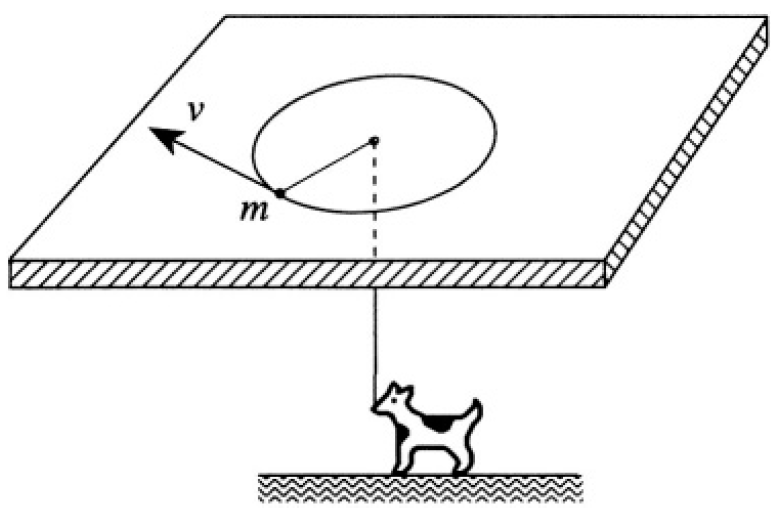
Figure 1.1
SOLUTION
In order to keep the mass traveling in a circular orbit of radius r, you must apply a force F equal to the mass times its centripetal acceleration v2/r
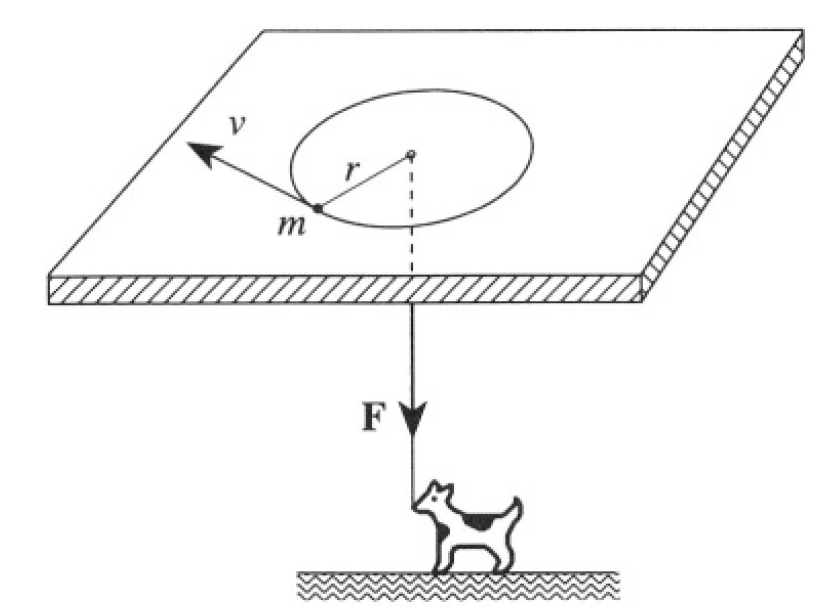
Figure 1.2
(see Figure 1.2). Pulling on the rope exerts no torque on the rotating mass, so the angular momentum l = mvr is conserved. Therefore
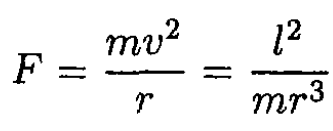
Then the work W necessary to move the mass from its initial orbit of radius R to its final orbit of radius R/2 is
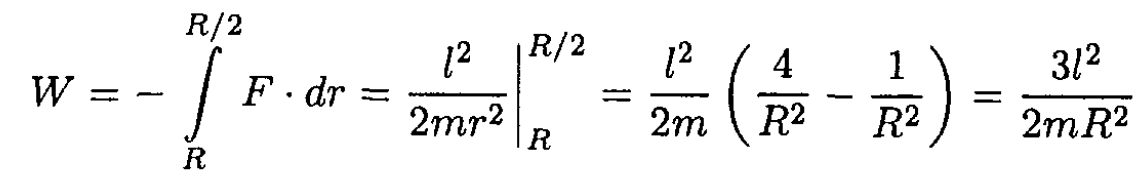
Solving in terms of E0:
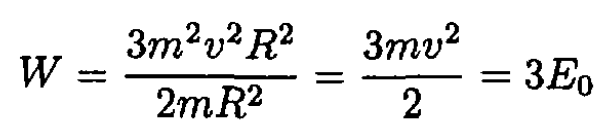
 الاكثر قراءة في مواضيع اخرى
الاكثر قراءة في مواضيع اخرى
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة


